Question

A chord of a circle of radius 15cm subtends an angle of ${60^ \circ }$ at the centre. Find the areas of the corresponding minor and major segments of the circle. (use $\pi = 3.14$ and $\sqrt 3 = 1.73$)

Answer 1

We will first calculate the area of the sector formed by the radius subtending an angle of ${60^ \circ }$ at the centre. Then, find the triangle formed by the chord and the radii of the circle. Now, we can calculate the area of the minor segment subtracting the area of the triangle from the area of the sector. Next, find the area of the circle and subtract the area of the minor segment to find the area of the major segment.

Complete step-by-step answer:
We are given that the radius of the circle is 15cm.

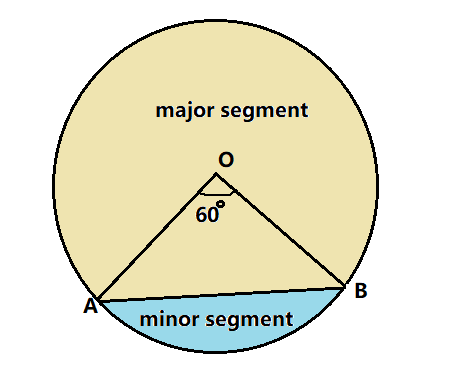
We will first calculate the area of the minor sector of the circle.
Also, area of a sector of the circle is given by $\pi {r^2} \times \dfrac{\theta }{{360}}$, where $\theta$ is angle of the sector formed.
Let us first calculate the area of the sector formed by an arc which makes an angle of ${60^ \circ }$ at the centre.
On substituting the value of $r = 15$, $\theta = {60^ \circ }$ and $\pi = 3.14$ in the formula for the area of the sector, we get,
$\left( {3.14} \right){\left( {15} \right)^2} \times \dfrac{{60}}{{360}}$
On simplifying and solving the above expression, we get,
$\left( {3.14} \right){\left( {15} \right)^2} \times \dfrac{1}{6} \\\ \Rightarrow \left( {3.14} \right)\left( {225} \right)\dfrac{1}{{16}} \\\ \Rightarrow 117.75c{m^2} \\\$
Thus, the area of the sector formed by the minor sector AOB is $117.75c{m^2}$
Now, the area of the segment can be calculated by subtracting the area of $\vartriangle AOB$ from the area of the sector.
In $\vartriangle AOB$, $AO = OB$ as the sides of the triangle are radius.
Then, angles opposite to equal sides are equal, hence, $\angle OAB = \angle OBA$
Also, sum of all the angles is ${180^ \circ }$
Then,
$\angle OAB + \angle OBA + \angle AOB = {180^ \circ } \\\ \Rightarrow 2\angle OAB + {60^ \circ } = {180^ \circ } \\\ \Rightarrow 2\angle OAB = {120^ \circ } \\\ \Rightarrow \angle OAB = {60^ \circ } \\\$
Hence, all the angles of $\vartriangle AOB$ are equal, therefore, $\vartriangle AOB$ is an equilateral triangle.
As it is known that the area of the triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$, where $a$ is the length of the side of an equilateral triangle.
We can see that the length of the side is equal to the radius of the circle.
Hence, we can calculate the area of the triangle as AOB,
$\dfrac{{\sqrt 3 }}{4}{\left( {15} \right)^2}$
On substituting $\sqrt 3 = 1.73$, we get,
$\dfrac{{1.73}}{4}{\left( {15} \right)^2} = 97.3c{m^2}$
Now, the area of the major segment will be calculated by subtracting $97.3c{m^2}$ from $117.75c{m^2}$
Thus, the area of minor segment is $117.75 - 97.3 = 20.45c{m^2}$
Let us now calculate the area of the major segment.
We can calculate the area of the minor segment by subtracting the area of the minor segment from the area of the circle.
Let us now calculate the area of the given circle.
We know that the area of the circle is given by $\pi {r^2}$.
Then, area of given circle when the radius is 15cm is,
$A = \left( {3.14} \right){\left( {15} \right)^2} \\\ \Rightarrow A = 706.5c{m^2} \\\$
Now, subtract the area of the minor segment from the area of the circle to get the area of the major segment.
Hence, we have, $706.5 - 20.45 = 686.05c{m^2}$
Thus, area of the major segment is $686.05c{m^2}$

Note Many students get confused with the terms ‘segment’ and ‘sector’ and find the area of the sectors instead of segment, which gets incorrect. A segment is formed by the chord and the arc of the circle, whereas a sector is formed by the arc and two radii of the circle.