Question

A chimney of $20\text{ }m$ height, standing on the top of the building subs tends an angle whose tangent is $\dfrac{1}{6}$ at a distance $70m$ from the foot of the building. The height of the building is

Answer 1

We apply trigonometry height & distance formula. In which we use either $\tan \theta ,\sin \theta$ or $\cos \theta$ if our perpendicular other is base. This kind of question is used to find the height and distance of things .

Formula used:
$Tan\theta =\dfrac{\text{perpendicular}}{\text{base}}$

Complete step-by-step answer:
__
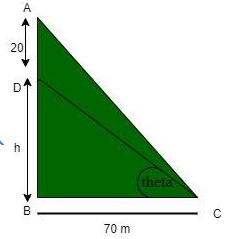
$\tan \theta =\dfrac{1}{6}$ (given)
AD$=20m$ (given)
BC=$70m$ (given)
Let us assume that the height of the building is h.
In $\vartriangle \text{ABC}$
$\Rightarrow Tan\theta =\dfrac{\text{perpendicular}}{\text{base}}$
$\Rightarrow \dfrac{1}{6}=\dfrac{h+20}{70}$
$\Rightarrow 70=6\left( h+20 \right)$(Cross multiply)
$\Rightarrow$ 70=6h+120
$\Rightarrow$ -120+70=6h
$\Rightarrow$ -50=6h
$\Rightarrow \dfrac{-50}{6}=h$ not possible as height can’t be negative or it’s a basement.

Additional information:
$\tan \theta =\dfrac{1}{6}$ that means $0<\theta <30$ (at least)
But the distance from the foot is $70m$ or if $\tan \theta =1$ then we can solve it.

Note: Please note that the height of building is negative which is not possible or it has to be underground and $\tan =\dfrac{1}{6}$ which is less than 1 that measures which is again a contradiction in either $\tan \theta$ has more than 1 value or distance has to be changed.