Question

A chimney 20 meters high standing on top of a building subtends an angle whose tangent is $\dfrac{1}{6}$ at a distance 70m from the foot of the building. Find the height of the building.

Answer 1

First, draw the figure on the base of the data provided. Then find the value of $\tan \beta$ from triangle BCD. After that, find the value of $\tan \alpha$ from the triangle ABC by using the formula $\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}$. After that substitute the values and do simplification to get the desired result.

Complete step-by-step solution:
First, draw the figure of the triangle using the given sides and angles.
The figure will somehow look like this,

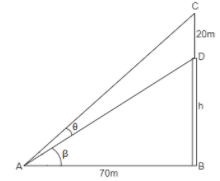
Where CD is the length of the chimney DB is the length of the house AB is the distance between the foot of the building and the point of elevation and $\theta ,\beta$ is the angle of elevation.
It is already given that $CD = 20m$ and $AB = 70m$.
Let us take the height of the building be h meters.
Now in $\Delta ACD$, it is already given that
$\tan \theta = \dfrac{1}{6}$................….. (1)
In $\Delta ABD$,
$\tan \beta = \dfrac{{BD}}{{AB}}$
Substitute the values,
$\Rightarrow \tan \beta = \dfrac{h}{{70}}$..............….. (2)
In $\Delta ABC$,
$\tan \left( {\theta + \beta } \right) = \dfrac{{BC}}{{AB}}$
Since $BC = BD + DC$. Then,
$\Rightarrow \tan \left( {\theta + \beta } \right) = \dfrac{{BD + DC}}{{AB}}$
Substitute the values,
$\Rightarrow \tan \left( {\theta + \beta } \right) = \dfrac{{h + 20}}{{70}}$
As we know that $\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}$. So,
$\Rightarrow \dfrac{{\tan \theta + \tan \beta }}{{1 - \tan \theta \tan \beta }} = \dfrac{{h + 20}}{{70}}$
Substitute the values from equation (1) and (2),
$\Rightarrow \dfrac{{\dfrac{1}{6} + \dfrac{h}{{70}}}}{{1 - \dfrac{1}{6} \times \dfrac{h}{{70}}}} = \dfrac{{h + 20}}{{70}}$
Take LCM on both numerator and denominator,
$\Rightarrow \dfrac{{\dfrac{{70 + 6h}}{{420}}}}{{\dfrac{{420 - h}}{{420}}}} = \dfrac{{h + 20}}{{70}}$
Cancel out the common factors,
$\Rightarrow \dfrac{{70 + 6h}}{{420 - h}} = \dfrac{{h + 20}}{{70}}$
Cross multiply the terms,
$\Rightarrow 70\left( {70 + 6h} \right) = \left( {h + 20} \right)\left( {420 - h} \right)$
Multiply the terms on both sides,
$\Rightarrow 4900 + 420h = 420h - {h^2} + 8400 - 20h$
Simplify the terms,
$\Rightarrow 4900 = - {h^2} + 8400 - 20h$
Move all terms to one side,
$\Rightarrow {h^2} + 20h - 3500 = 0$
We can write 20 as (70 – 50)
$\Rightarrow {h^2} + \left( {70 - 50} \right)h - 3500 = 0$
Open the brackets and multiply the terms,
$\Rightarrow {h^2} + 70h - 50h - 3500 = 0$
Take common factors from the equation,
$\Rightarrow h\left( {h + 70} \right) - 50\left( {h + 70} \right) = 0$
Take common factors from the equation,
$\Rightarrow \left( {h + 70} \right)\left( {h - 50} \right) = 0$
Then,
$\Rightarrow h = - 70,50$
Since height cannot be negative. So,
$\therefore h = 50m$

The height of the building is 50m

Note: Sketching figures is a must in these height and distance problems. It gives you a better understanding of what values you have and what you need to find out. 20m is the height of the chimney given students often make the mistake to consider it as a height of BC i.e., the height of the building + chimney.