Question
Question: A child with mass \(m\) is standing at the edge of a disc with moment of inertia \(I\), radius \(R\)...
A child with mass m is standing at the edge of a disc with moment of inertia I, radius R, and initial angular velocity ω. See the figure given below. The child jumps off the edge of the disc with tangential velocity v with respect to the ground. The new angular velocity of the disc is:
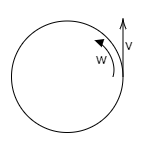
(A) IIω2−mv2
(B) I(I+mR2)ω2−mv2
(C) IIω−mvR
(D) I(I+mR2)ω−mvR
Solution
The new angular velocity can be determined by using the initial angular momentum equation and the final angular momentum equation. By equating the two angular momentum equations, the new angular velocity can be determined.
Complete step by step answer:
Given that,
The mass of the child is given by, m,
The moment of inertia of the disc is, I,
The radius of the disc is given by, R,
The initial angular velocity of the disc is, ω,
The tangential velocity of the disc is, v,
Assume the final angular velocity of the disc is, ω′.
The angular momentum is equal to the product of the moment of inertia and angular velocity. Here angular momentum is the sum of the angular momentum of the disc and the angular momentum of the child, then
The initial angular momentum is given by, Li=Iω+mR2ω................(1)
Where, Li is the initial angular momentum, I is the moment of inertia, ω is the angular velocity, m is the mass of the child and R is the radius of the disc.
The final angular momentum is given by, Lf=Iω′+mvR................(2)
Where, Li is the initial angular momentum, I is the moment of inertia, ω is the angular velocity, m is the mass of the child, R is the radius of the disc and v is the tangential velocity.
By equating the equation (1) and equation (2), then
Iω+mR2ω=Iω′+mvR
By taking the common terms in the above equation, then
(I+mR2)ω=Iω′+mvR
By rearranging the terms from the above equation, then
(I+mR2)ω−mvR=Iω′
By rearranging the terms from the above equation, then
ω′=I(I+mR2)ω−mvR
Thus, the above equation shows the new angular velocity of the disc.
Hence, the option (D) is the correct answer.
Note: In the initial angular momentum, it is the sum of the angular momentum of the sum of the disc and the angular momentum of the child. In the final angular momentum, it is the sum of the angular momentum of the disc and the angular momentum when the child jumps with tangential velocity.
