Question

A charged ring of radius 0.5 m has a 0.002$\pi$m gap. If the ring carries a charge of +1 C, the electric field at the center is:
A. $7.5 \times {10^7}N{C^{ - 1}}$
B. $7.2 \times {10^7}N{C^{ - 1}}$
C. $6.2 \times {10^7}N{C^{ - 1}}$
D. $6.5 \times {10^7}N{C^{ - 1}}$

Answer 1

Hint: In this question, we have to remember the concept of finding the electric field due to a circular loop of charge. We have to remember that if charge is not present in the gap, the electric field at the center would be because of the rest of the ring.

Formula used: $dq = \dfrac{q}{{2\pi a}}dl$, $\dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{q}{{{x^2}}}.$

Complete step-by-step solution -
__
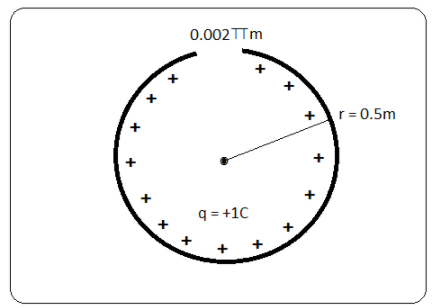
Given that, the radius of ring = 0.5m and gap = $0.002\pi m$ and the ring carries a charge of +1 C.
We know that charge on the elementary length is given by,
$\Rightarrow dq = \dfrac{q}{{2\pi a}}dl$ .
Now, the charge on the elementary length opposite to the gap will be,
$\Rightarrow q = \dfrac{Q}{{2\pi \times r}} \times gap \\\ \Rightarrow q = \dfrac{1}{{2\pi \times 0.5}} \times 0.002\pi \\\ \Rightarrow q = 2 \times {10^{ - 3}}C \\\$.
Now, suppose that the charge is also present in the gap so the electric field at the centre will be zero.
So, if the charge is not present in the gap, the electric field at the centre would be because of the rest of the ring, which should be equal and opposite to the electric field produced due to the charge in the gap.
We know that, electric field at a distance x = $\dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{q}{{{x^2}}}.$ ……….(i)
Here, q = $2 \times {10^{ - 3}}C$ and x = 0.5m and the factor, $\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}.$
Putting these values in equation (i), we get
$\Rightarrow E = 9 \times {10^9}N{m^2}{C^{ - 2}} \times \dfrac{{2 \times {{10}^{ - 3}}C}}{{(0.5 \times 0.5){m^2}}}. \\\ \Rightarrow E = 9 \times {10^9}N{m^2}{C^{ - 2}} \times \dfrac{{2 \times {{10}^{ - 3}}C}}{{0.25{m^2}}} \\\$
Solving this, we get
$\Rightarrow E = 7.2 \times {10^7}N{C^{ - 1}}.$
Hence, the electric field at the centre is $7.2 \times {10^7}N{C^{ - 1}}$.
Therefore, the correct answer is option (B).

Note: Whenever we are asked such types of questions, we have to remember some basic points of finding the electric field due to a circular charged ring. First we have to find out the charge on the elementary length and then we will use that value of charge to find out the electric field using the formula. Then the electric field due to the elementary length will be that electric field. Through this we will get the answer.