Question

A charged particle q is shot towards another charged particle $Q$ which is fixed, with a speed $v$ . It approaches $Q$ upto a closest distance of $r$ and then returns. If $q$ was given a speed $2v$ , find the closest distance of approach.

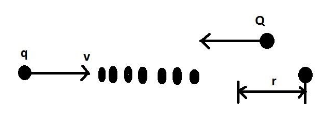
(A) $r$
(B) $2r$
(C) $r/2$
(D) $r/4$

Answer 1

Hint : We need to use the law of conservation of energy to solve this problem. We need to equate the total initial and final energy of the system and then by substituting the values of the initial and final potential energy, we will be able to calculate the distance of closest approach.

Formula Used: The following formulae are used to solve this question, ${\left( {P.E. + K.E.} \right)_{initial}} = {\left( {P.E. + K.E.} \right)_{final}}$ where $K.E.$ and $P.E.$ are the kinetic energy and potential energy of a body respectively.
$\Rightarrow K.E. = \dfrac{1}{2}m{v^2}$ where $m$ is the mass and $v$ is the velocity of a body.
$\Rightarrow P.E. = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$ where $Q$ and $q$ are two charges and $r$ is the closest distance of approach.

Complete step by step answer
Kinetic energy is the energy an object possesses because of its motion. This energy is dependent on the velocity of the object squared.
$\Rightarrow K.E. = \dfrac{1}{2}m{v^2}$ where $m$ is the mass and $v$ is the velocity of a body.
Potential energy is energy stored as the result of its position. The electric potential energy of any given system of charges is the work done by an external agent in bringing the charge from infinity to the present configuration in an electric field.
According to the law of conservation of energy, energy is neither created nor destroyed. It is only transformed from state to another.
Thus for the given system, it can be written that,
$\Rightarrow {\left( {P.E. + K.E.} \right)_{initial}} = {\left( {P.E. + K.E.} \right)_{final}}$ where $K.E.$ and $P.E.$ are the kinetic energy and potential energy of a body respectively.
The particle carrying charge $q$ comes to rest momentarily at $r$ distance from the particle carrying $Q$ charge. At this point all the kinetic energy of $q$ is transformed into potential energy.
Thus, $K.E. = \dfrac{1}{2}m{v^2} = P.E.$ and
$\Rightarrow P.E. = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$ where $Q$ and $q$ are two charges and $r$ is the closest distance of approach.
$\therefore \dfrac{1}{2}m{v^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$
Therefore the distance of closest approach is given by the equation above:
$\therefore \dfrac{1}{2}m{v^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$
$\Rightarrow r = \dfrac{{qQ}}{{4\pi {\varepsilon _0}}} \cdot \dfrac{2}{{m{v^2}}}$
Thus the relation between $r$ and $v$ can be derived from here.
$r\alpha \dfrac{1}{{{v^2}}}$ , that is, $r$ varies inversely with the square of velocity $v$ .
Hence, if $v = 2v$ , then, the distance of closest approach r becomes
$$ $\dfrac{r}{4}$ .
$\therefore$ The correct answer is Option D.

Note
Another method to solve this question is given as,
So far, we know that, $\dfrac{1}{2}m{v^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$ ………………………….(1)
This is equation (1).
Let us assume $R$ is the closest distance of approach when charge $q$ possesses a velocity of $2v$ .
Thus, substituting the values of velocity and distance in the equation,
$\dfrac{1}{2}m{\left( {2v} \right)^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{R}$
$\Rightarrow 4 \times \dfrac{1}{2}m{v^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{R}$ ………………………………..(2)
This is equation (2).
Thus the value of $R$ is found by solving equation (1) and (2) as,
$\dfrac{1}{4} = \dfrac{r}{R}$
$\Rightarrow R = \dfrac{r}{4}$
$\therefore$ The correct answer is Option D.