Question

A charged particle of mass $'m'$ and charge $'q'$ moving under the influence of uniform electric field $E\vec i$ and a uniform magnetic field $B\vec k$ follows a trajectory from point P to Q as shown in figure. The velocities at P and Q are respectively, $v\vec i$ and $- 2v\vec j$ . Then which of the following statements (A, B, C, D) are the correct? (Trajectory shown in schematic and not to scale)
(A) $E = \dfrac{3}{4}\left( {\dfrac{{m{v^2}}}{{qa}}} \right)$
(B) Rate of work done by the electric field at P is $\dfrac{3}{4}\left( {\dfrac{{m{v^3}}}{a}} \right)$
(C) Rate of work done by both the field at Q is zero
(D) The difference between the magnitude of angular momentum of the particle at P and Q is $2mav$ .

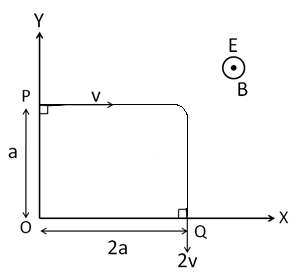
A. (A), (B), (C), (D)
B. (A), (C), (D)
C. (B), (C), (D)
D. (A), (B), (C)

Answer 1

Hint : To solve this question, we need to use the work energy theorem between the points P and Q. The rate of work done can be found out by using the formula for the power. Also, the difference between the magnitudes of the angular momentum can be calculated by using its formula.

Formula used: The formulae which are used to solve this question are given by
${F_E} = qE$ , here ${F_E}$ is the force applied by the electric field $E$ on a charge $q$ .
$W = \int\limits_A^B {Fds\cos {{\theta }}}$ , here $W$ is the total work done by a force $F$ in displacing a particle from $A$ to $B$ , $ds$ is the displacement, and ${{\theta }}$ is the angle between $ds$ and $F$ .
$P = FV\cos {{\theta }}$ , here $P$ is the power supplied by a force $F$ on a particle moving with a velocity $V$ , and ${{\theta }}$ is the angle between the force and the velocity.

Complete step by step answer
We know that both the electric and the magnetic forces are conservative forces. Since the particle moves in a region of the electric and the magnetic fields, so the energy of the particle remains conserved between the points P and Q. So from the work energy theorem we have
${W_{PQ}} = {K_Q} - {K_P}$ ………………………..(1)
The work done ${W_{PQ}}$ is the total work done by the electric and the magnetic force on the charged particle.
$\therefore {W_{PQ}} = {W_E} + {W_B}$ ………………………..(2)
Now, work done by the electric field is ${W_E} = \int\limits_P^Q {{F_E}ds\cos {{\theta }}}$
We know that ${F_E} = qE$ . So we get
${W_E} = \int\limits_P^Q {qEds\cos {{\theta }}}$
${W_E} = qE\int\limits_P^Q {ds\cos {{\theta }}}$ ………………………..(3)
As the electric field is parallel to the $x$ -axis, along which the displacement of the particle is $2a$ , so we have $\int\limits_P^Q {ds\cos {{\theta }}} = 2a$
So from (3) we have
${W_E} = 2aqE$ ………………………..(4)
Also, the work done by magnetic field is ${W_B} = \int\limits_P^Q {{F_B}ds\cos {{\theta }}}$
As we know that the magnetic force is always perpendicular to the motion of the charged particle, so the work done by the magnetic force is always equal to zero.
$\therefore {W_B} = 0$ ………………………..(5)
Substituting (4) and (5) in (2) we get
${W_{PQ}} = 2aqE$ ………………………..(6)
Now, the kinetic energy at point P is
${K_P} = \dfrac{1}{2}m{v^2}$ ………………………..(7)
Also, the kinetic energy at at Q is
${K_Q} = \dfrac{1}{2}m{\left( {2v} \right)^2}$
$\Rightarrow {K_Q} = 2m{v^2}$ ………………………..(8)
Substituting (6) (7) and (8) in (1) we get
$2aqE = 2m{v^2} - \dfrac{1}{2}m{v^2}$
$\Rightarrow 2aqE = \dfrac{3}{2}m{v^2}$
Dividing by $2aq$ we get
$E = \dfrac{3}{4}\left( {\dfrac{{m{v^2}}}{{qa}}} \right)$ ………………………..(9)
Hence, the statement (A) is correct.
Now, we know that the rate of work done is equal to the power which is given by
$P = FV\cos {{\theta }}$ ………………………..(10)
At P, the velocity of the charged particle is $v$ parallel to the electric field. So the power supplied by the electric field is given by
${P_E} = qEv$
From (9)
${P_E} = \dfrac{3}{4}\left( {\dfrac{{m{v^3}}}{a}} \right)$
Hence, the statement (B) is also correct.
As we know that the magnetic force is always perpendicular to the motion of the charged particle. So we have ${{\theta }} = {90^ \circ }$ . So from (10) we get
${P_B} = 0$
Hence, the statement (C) is also correct.
Now, the angular momentum about O at P is given by
${L_P} = mav$
Also, the angular momentum at Q is given by
${L_Q} = m\left( {2a} \right)\left( {2v} \right) = 4mav$
So the difference is given by
$L = {L_Q} - {L_P} = 3mav$
Hence the statement (D) is incorrect.
Thus the correct statements are (A), (B) and (C).
Hence, the correct answer is option D.

Note
In this question we were not given the point about which the angular momentum was supposed to be calculated. So we assumed that point to be the origin while doing the calculation.