Question

A charged particle of charge Q is held fixed and another charged particle of mass m and charge q (of the same sign) is released from a distance r. The impulse of the force exerted by the external agent on the fixed charge by the time distance between Q and q becomes 2r is:
a.) $\sqrt{\dfrac{Qq}{4\pi {{\varepsilon }_{0}}mr}}$
b.) $\sqrt{\dfrac{Qqm}{4\pi {{\varepsilon }_{0}}r}}$
c.) $\sqrt{\dfrac{Qq}{\pi {{\varepsilon }_{0}}mr}}$
d.) $\sqrt{\dfrac{Qq}{2\pi {{\varepsilon }_{0}}mr}}$

Answer 1

In the above question we need to find out the velocity of the particle. When a particle moves, it possesses kinetic energy. When the charge particle moves between the two points under the influence of a potential either it gains or loses potential energy. In the above case it will lose its potential energy which will be seen in the form of kinetic energy.

Complete answer:
To solve this question, first we will make a diagram to understand where each charge is placed an at what distance, making diagram always makes the problem easy to solve

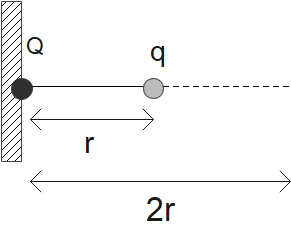
According to the law of conservation of energy, the total energy always remains conserved and Energy can neither be created nor be destroyed. Using this simple law we know that the sum of kinetic energy and potential energy always remains conserved.
Net Impulse (I) = $\int\limits_{0}^{t}{F.dt=m\Delta {{{\vec{v}}}_{q}}}$
Initial Potential energy for charge “q” is ${{U}_{i}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{r}$
Final potential energy ${{U}_{f}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{2r}$
As the charge Particle “q” is only under the effect of electrostatic forces, this means that the mechanical energy is conserved.
Final Kinetic Energy ${{K}_{f}}={{U}_{i}}-{{U}_{f}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{2r}$
kinetic energy is defined as ${{K}_{f}}=\dfrac{1}{2}mv_{q}^{2}$
Therefore, ${{v}_{q}}=\sqrt{\dfrac{2{{K}_{f}}}{m}}$
Impulse $I=m{{v}_{q}}=\sqrt{2m{{K}_{f}}}=\sqrt{\dfrac{Qqm}{4\pi {{\varepsilon }_{0}}r}}$

Hence, we can conclude that option (b) $\sqrt{\dfrac{Qqm}{4\pi {{\varepsilon }_{0}}r}}$ is the correct answer.

Note:
It is to be noted that all the physical quantities have to be expressed in terms of SI units. The basic idea of solving the above question was conservation of energy. Though the above scenario might not be according to reality, if we know how the energy gets transformed into other forms, we will be in position to determine the answer more precisely.