Question: A charged particle is projected from A in a non-uniform magnetic field as shown in the figure. ![]...

Question

A charged particle is projected from A in a non-uniform magnetic field as shown in the figure.

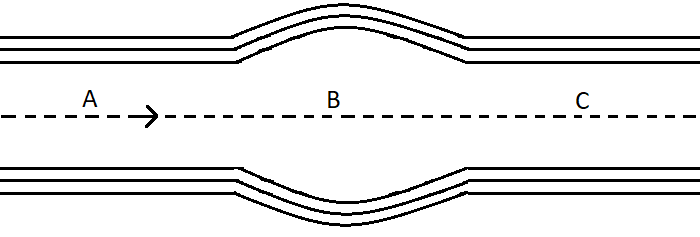
The magnitudes of the velocities at point A, B and C respectively during the motion is
(A) Maximum at A and C
(B) Maximum at B
(C) Minimum at A and C
(D) Equal at A, B and C

Answer 1

Solution

Here at every point the magnetic field is perpendicular to the displacement of the particle. The work done is the dot product of the force and the displacement. Hence the value of the work done is zero. So there is no change in kinetic energy and hence the velocity is the same at all the points.

Complete step by step solution:
In the question, we are given that the charged particle is projected in a non uniform magnetic field from the point A. Now the direction of the displacement of the charged particle is perpendicular to the direction of the magnetic field. The force on the charged particle is the cross product of the velocity and the magnetic field. So the force on the particle will be perpendicular to both the velocity and the magnetic field.
The work done is the dot product of the force and the displacement.
$\Rightarrow W = \vec F \cdot \vec S$
We can break this up as,
$\Rightarrow W = FS\cos \theta$
Now since the force and the displacement are perpendicular to each other, so the angle between them is $90^\circ$ .
So we have, $W = FS\cos 90$
Therefore the work done is zero.
This work done is the change in the kinetic energy at the different points. Now the kinetic energy at the different points is directly proportional to the square of the velocities at the different points A, B and C.
Therefore, since the kinetic energy is the same at the different points, the velocity is the same at the three points.
Hence, the magnitudes of the velocities are equal at the points A, B and C.
So the option (D) is correct.

Note:
Non-uniform magnetic field is where the magnitude of the magnetic field changes with space and time. The work done by a particle in such a magnetic field is proportional to the force that the charged particle experiences in that field.