Question
Question: A charge \[Q\] is uniformly distributed over a long rod AB of length \[L\] as shown in the figure. T...
A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
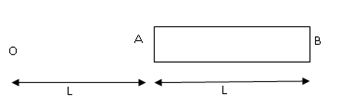
8πε0LQ
4πε0L3Q
4πε0Lln2Q
4πε0LQln2
Solution
We are asked to find the potential at point O due to rod AB. First find the line charge density of the rod. Take a small element from the rod and find its potential at the given point. Use this potential due to an element of rod AB to find the potential due to the whole rod AB at the given point.
Complete step by step answer:
Given, the length of the rod AB is L and charge Q is uniformly distributed over the rod AB.
Let λ be the line charge density, line charge density can be written as,
λ=LengthCharge
⇒λ=LQ
First, we take a small element dx of the rod AB at a distance x from point O.
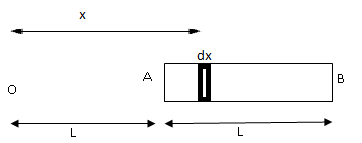
Self-made diagram
Potential at O due to the element dx can be written as,
dV=4πε01xQ (i)
For length L, line charge density is, λ=LQ and for dx length line charge density will be
λ=dxQ
⇒Q=λdx
Now, substituting this value of Q in equation (i), we get
dV=4πε01xλdx (ii)
This is the potential due to a small element dx. To find the potential due to the whole rod AB we integrate equation (iii) from L to 2L. We take L to 2Lbecause the distance between point O and one end of the rod is 2L and the other end is L .
