Question

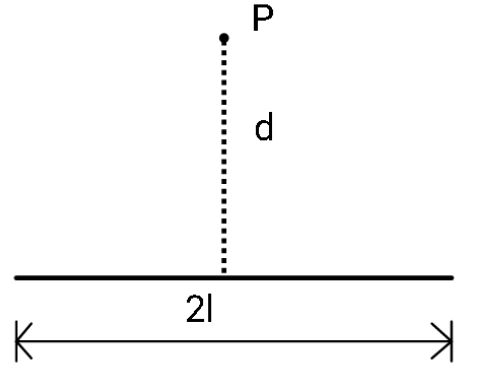
A charge q is uniformly distributed along an insulating straight wire of length 2l as shown in fig. Find the expression for electric potential at a point located at a distance d from the distribution along its perpendicular bisector:

A. $V = \dfrac{1}{4 \pi \epsilon_0 }. \dfrac{q}{l} \ln \left( \dfrac{\sqrt{l^2 + d^2} + l}{\sqrt{l^2 + d^2} - l} \right)$
B. $V = \dfrac{1}{4 \pi \epsilon_0 }. \dfrac{q}{2l} \ln \left( \dfrac{\sqrt{l^2 + d^2} - l}{\sqrt{l^2 + d^2} + l} \right)$
C. $V = \dfrac{1}{4 \pi \epsilon_0 }. \dfrac{q}{2l} \ln \left( \dfrac{\sqrt{l^2 + d^2} + l}{\sqrt{l^2 + d^2} - l} \right)$
D. $V = \dfrac{1}{4 \pi \epsilon_0 }. \dfrac{q}{4l} \ln \left( \dfrac{\sqrt{l^2 + d^2} + l}{\sqrt{l^2 + d^2} - l} \right)$

Answer 1

Start by writing down the potential due to a point charge. Integration on the line charge has to be performed in order to know the potential at point P. So, pick an element of the wire (dx) and find its potential just like the potential for a point charge.
Formula used:
The potential at a distance r from a point charge q is given as:
$V = \dfrac{1}{4 \pi \epsilon_0} \dfrac{q}{r}$.

Complete step-by-step solution:
$dV = \dfrac{1}{4 \pi \epsilon_0} \dfrac{\lambda dx}{r}$ .
Notice that the charge of the element is $\lambda$ dx (as density times length is a charge).
Now, the distance of this element from P (hypotenuse) can be written as:

$r = \sqrt{d^2 + x^2}$
(from Pythagoras theorem).
Substituting the value of r and integrating on both sides we get:
$V = \dfrac{\lambda }{4 \pi \epsilon_0} \int_{-l}^{+l} \dfrac{dx}{\sqrt{d^2 + x^2}}$
For there types of integrals, we use the formula for special integrals and obtain the result as:
$V = \dfrac{\lambda }{4 \pi \epsilon_0} \left[ \ln ( x + \sqrt{d^2 + x^2} )\right] \bigg|_{-l}^{+l}$
Substituting the limits in place of x gives us:
$V = \dfrac{\lambda }{4 \pi \epsilon_0} \ln \left[ \dfrac{ l + \sqrt{d^2 + l^2} }{ -l + \sqrt{d^2 + l^2} }\right]$
As we used the formula
$\ln m - \ln n = \ln \dfrac{m}{n}$ .
Now upon substituting the value of $\lambda$ we see our required expression as:
$V = \dfrac{1}{4 \pi \epsilon_0} . \dfrac{q}{2l} \ln \left[ \dfrac{ \sqrt{d^2 + l^2} +l }{ \sqrt{d^2 + l^2} -l}\right]$
Therefore, the correct answer is option (C).

Note: We performed integration from -l to +l assuming that the center of the wire is placed at the origin. As the length of the wire is 2l, the wire must extend +l along the +x direction and -l along the x-direction.