Question

A charge q is placed at the centre of the line joining two equal charges Q. Show that the system of three charges will be in equilibrium if $q=-\dfrac{Q}{4}$ .

Answer 1

As a first step you could depict the situation in a diagram. You could consider any one of the three charges and then, you may recall Coulomb's law and apply it on that charge to get the force due to the other two charges. By superposition principle, we will get the net force on that charge and for equilibrium condition, you could equate it to zero and thus get the required proof.

Formula used:
Coulomb’s law,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{QQ'}{{{r}^{2}}}$

Complete answer:
In the question, we are given a system of three charges. Two of them are equal and are placed at the end of a line AC. There is also a charge q that is placed in between them exactly at the midpoint of the line joining the other two charges of charge Q. We could depict the situation as given below.

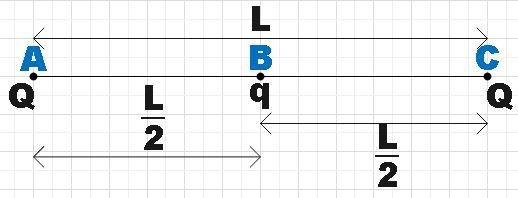
We are supposed to prove that at equilibrium the charge q would be given by,
$q=-\dfrac{Q}{4}$
Let us recall that a system of charges is said to be in equilibrium, when the net force acting on each charge is found to be zero. Now, let us consider the charge Q kept at the point A which is at a distance of L from the charge Q at point C and at a distance of $\dfrac{L}{2}$ from charge q at point B.
You may recall that by coulomb’s law, the force on a charge Q due to another charge Q’ at a distance r is given by,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{QQ'}{{{r}^{2}}}$
Now the force on Q at A due to Q at C is given by,
${{F}_{AC}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{L}^{2}}}$
The force on Q at A due to q at B will be,
${{F}_{AB}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{\left( \dfrac{L}{2} \right)}^{2}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{4Qq}{{{L}^{2}}}$
Now, by principle of superposition, the net force on Q at point A can be given by,
$F={{F}_{AB}}+{{F}_{AC}}$
$\Rightarrow F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{L}^{2}}}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{4Qq}{{{L}^{2}}}$
But we know that net force would be zero at equilibrium. So,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{L}^{2}}}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{4Qq}{{{L}^{2}}}=0$
$\Rightarrow \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{L}^{2}}}=-\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{4Qq}{{{L}^{2}}}$
$\therefore q=-\dfrac{Q}{4}$
Therefore, we found that the system of three charges will be in equilibrium if$q=-\dfrac{Q}{4}$ .

Note:
We shouldn’t necessarily choose charge Q at point A to prove this statement. We could select any of the other charges to prove the required condition as at equilibrium, net force on each charge is found to be zero. So, if we select either Q at C or q at B to prove this, we would end up with the same result.