Question
Question: A charge Q is placed at the centre of a square. If electric field intensity due to the charge at the...
A charge Q is placed at the centre of a square. If electric field intensity due to the charge at the corners of the square is E₁ and the intensity at the mid point of the side of square is E₂, then the ratio of E₁/E₂ will be
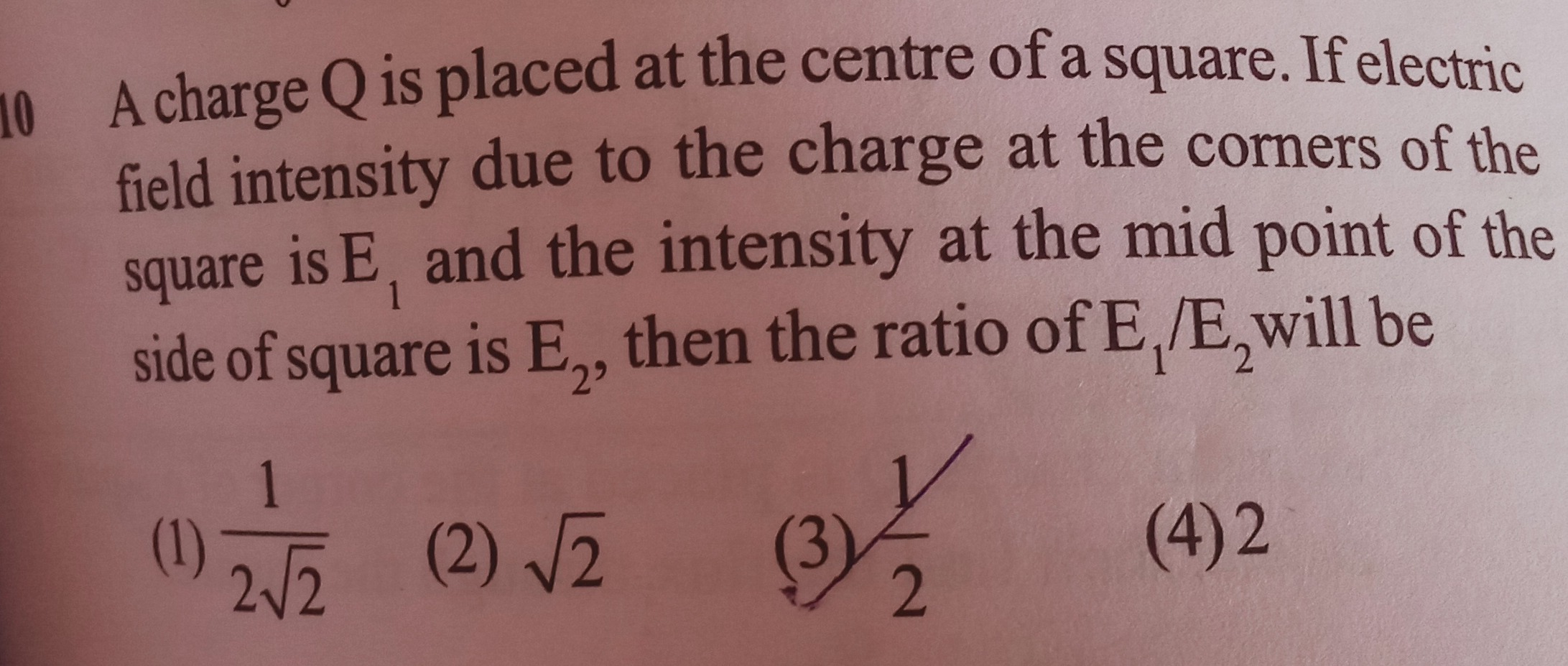
221
2
21
2
The ratio E₁/E₂ is 21.
Solution
Let the side length of the square be a. The charge Q is placed at the center of the square.
The distance from the center of the square to any corner (r1) is half the length of the diagonal. The diagonal of a square with side length a is a2+a2=a2.
So, r1=2a2=2a.
The electric field intensity at a corner is E1. Using the formula for the electric field due to a point charge E=r2kQ, where k=4πϵ01:
E1=r12kQ=(a/2)2kQ=a2/2kQ=a22kQ.
The distance from the center of the square to the midpoint of any side (r2) is half the side length.
So, r2=2a.
The electric field intensity at the midpoint of a side is E2:
E2=r22kQ=(a/2)2kQ=a2/4kQ=a24kQ.
The ratio of E1 to E2 is:
E2E1=4kQ/a22kQ/a2=42=21.
The ratio E1/E2 is 21.
