Question
Question: A charge +Q is placed at each of the diagonally opposite corners of a square. A charge -q is placed ...
A charge +Q is placed at each of the diagonally opposite corners of a square. A charge -q is placed at each of the other diagonally opposite corners as shown. If the net electrical force on +Q is zero, then +Q−q is equal to
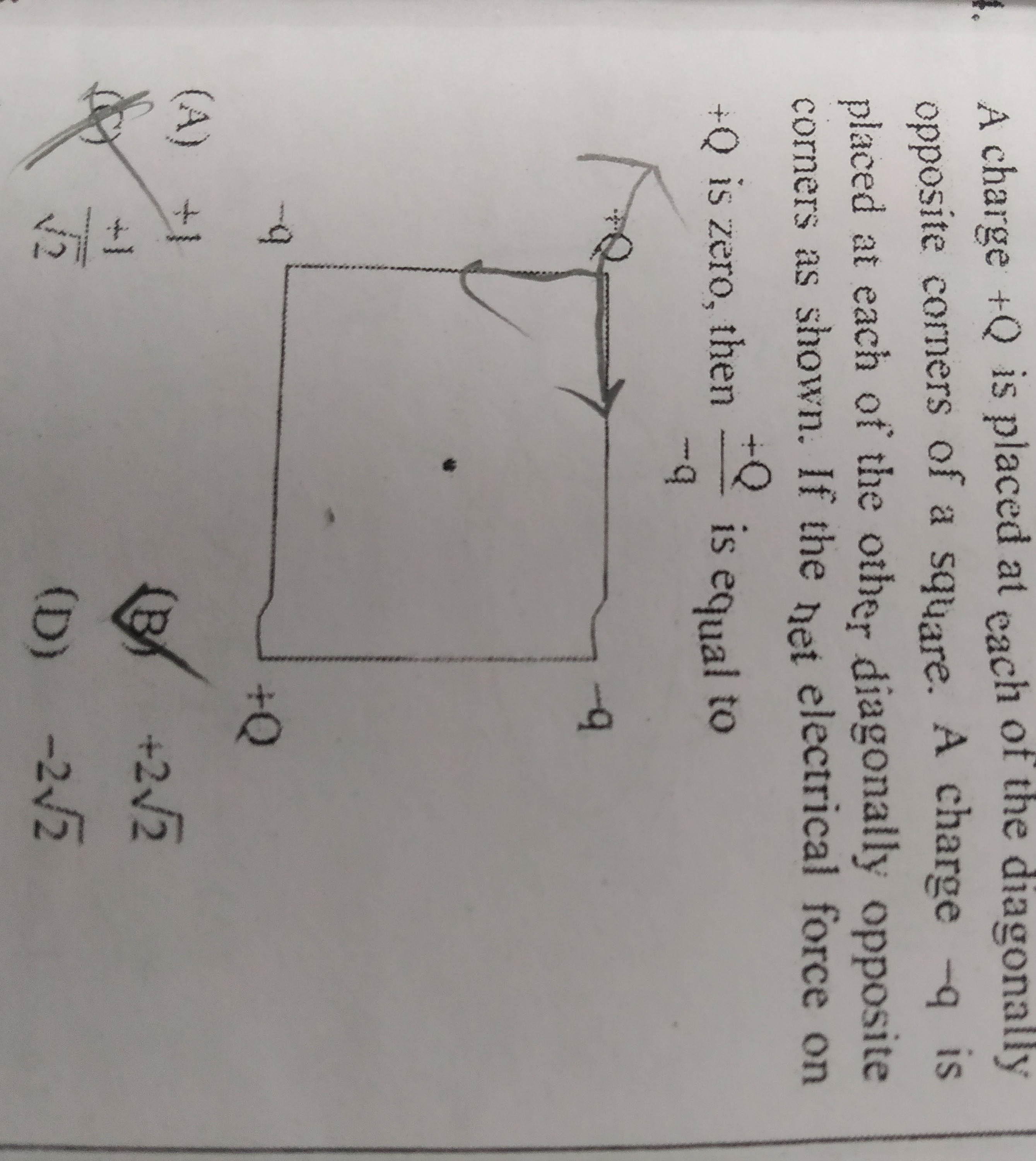
+1 2+1
+22
-22
22−1
Solution
To solve this problem, we need to consider the forces acting on one of the +Q charges due to the other charges. Let's denote the side length of the square as a.
-
Forces due to -q charges: Each -q charge exerts an attractive force on the +Q charge. The magnitude of each of these forces is given by Coulomb's law:
F=a2kQq
where k is Coulomb's constant. These forces are directed along the sides of the square towards the -q charges.
-
Force due to the other +Q charge: The other +Q charge exerts a repulsive force on the +Q charge. The distance between these charges is 2a (the diagonal of the square). The magnitude of this force is:
F′=2a2kQ2
This force is directed along the diagonal of the square, away from the other +Q charge.
-
Net Force: For the net force on +Q to be zero, the vector sum of the forces due to the two -q charges must be equal and opposite to the force due to the other +Q charge. The resultant force due to the two -q charges acts along the diagonal and has a magnitude of 2F=a22kQq.
Therefore, we must have:
a22kQq=2a2kQ2
-
Solving for -q/+Q: Simplifying the equation, we get:
2q=2Q
q=22Q
Since we are looking for the ratio +Q−q, and considering that the charges -q are negative, we have:
+Q−q=−221
