Question

A charge $q$ is moved along the axis of cylinder with constant velocity $v$. Choose the correct variation of flux through the surface / cylinder.

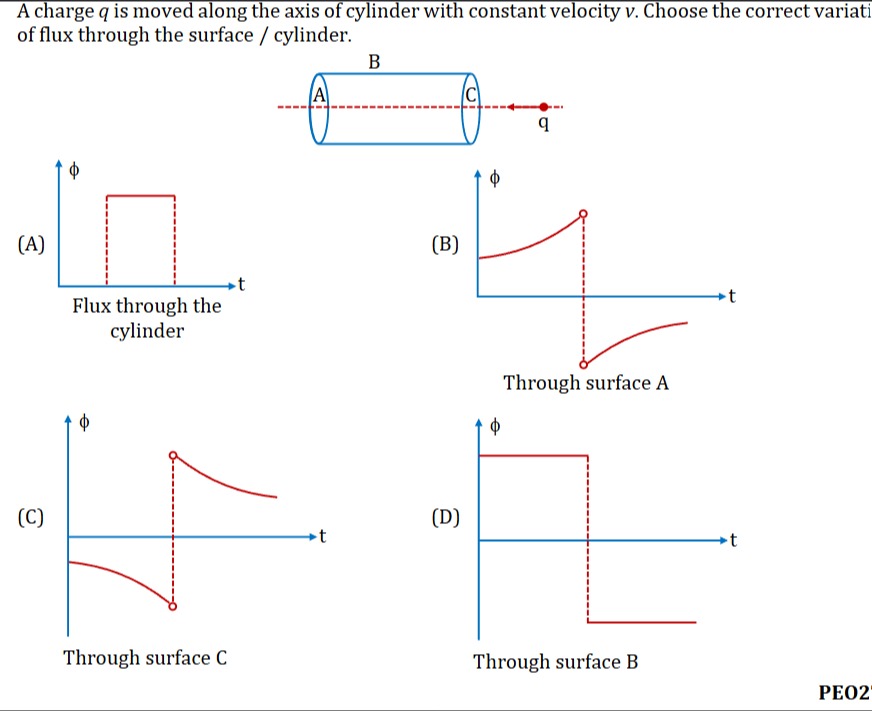
• A. Flux through the cylinder
• B. Through surface A
• C. Through surface C
• D. Through surface B

Answer 1

Answer: (A), (B), (C)

A, B, C

Answer 2

1. Flux through the entire cylinder (closed surface): According to Gauss's Law, the total flux through a closed surface is $\Phi_{total} = \frac{Q_{enclosed}}{\epsilon_0}$. When the charge $q$ is outside the cylinder, $Q_{enclosed} = 0$, so $\Phi_{total} = 0$. When the charge $q$ is inside the cylinder, $Q_{enclosed} = q$, so $\Phi_{total} = \frac{q}{\epsilon_0}$. As the charge moves along the axis, it enters the cylinder at some time $t_1$ and exits at some time $t_2$. Before $t_1$, $\Phi_{total} = 0$. Between $t_1$ and $t_2$, $\Phi_{total} = \frac{q}{\epsilon_0}$. After $t_2$, $\Phi_{total} = 0$. This describes a rectangular pulse for the total flux, matching option (A).

2. Flux through surface A (left end cap): Let the cylinder be along the x-axis. Surface A is at $x=0$. The flux through A is positive when the charge is to the right ($x_q > 0$) and negative when the charge is to the left ($x_q < 0$). As the charge moves from right to left, the flux through A transitions from positive to negative, matching the general behavior shown in option (B).

3. Flux through surface C (right end cap): Surface C is at $x=L$. The flux through C is negative when the charge is to the right of the cylinder ($x_q > L$) and positive when the charge is to the left of the cylinder ($x_q < L$). As the charge moves from right to left, the flux through C transitions from negative to positive, matching the general behavior shown in option (C).

4. Flux through surface B (curved lateral surface): The flux through the curved surface is complex and does not typically exhibit the sharp step-function behavior shown in option (D). Therefore, option (D) is incorrect.