Question

A channel 27m wide falls at a right angle into another channel 64m wide. The greatest length of the log that can be floated along this system of channels is
A. 120m
B. 125m
C. 100m
D. 110m

Answer 1

Hint: In this question, first we will make the diagram of the question. After this using a trigonometric function we will find the length of the log in terms of angle $\theta$. Now to find the maximum possible length of the log, we will differentiate the function which represents the length of log w.r.t $\theta$ and then equate it to zero. And finally use this result to find the length of the log.

Complete step-by-step answer:
The diagram of question is as follow:

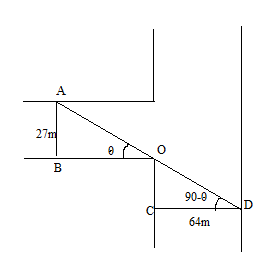
It is give that”
AB channel is vertical channel while channel CD is horizontal and we have to find the length of log AD.
In $\vartriangle$ABO, we know that trigonometric function $\sin \theta$ is given by:
$\sin \theta$=$\dfrac{{{\text{perpendicular}}}}{{{\text{Hypotenuse}}}}$
$\therefore$ $\sin \theta$ =$\dfrac{{27}}{{OA}}$.
OA = $\dfrac{{27}}{{\sin \theta }}$
In $\vartriangle$COD, we know that trigonometric function $\cos \theta$:
$\therefore$ OD =$\dfrac{{64}}{{\cos \theta }}$.
Therefore, the length of log as function of angle $\theta$ is:
Length of log =AD = OA +OD=$\dfrac{{27}}{{\sin \theta }}$+$\dfrac{{64}}{{\cos \theta }}$=$f(\theta )$
To get the maximum length of log, we will differentiate the function $f(\theta )$w.r.t. $\theta$ and equate it to zero.
i.e. ${f'}(\theta )$=0
$\Rightarrow \dfrac{{0 - 27\cos \theta }}{{{{\sin }^2}\theta }} + \dfrac{{0 - ( - 64\sin \theta )}}{{{{\cos }^2}\theta }}$ =0
$\Rightarrow \dfrac{{{{\sin }^3}\theta }}{{{{\cos }^3}\theta }} = \dfrac{{27}}{{64}}$
$\Rightarrow {\tan ^3}\theta = \dfrac{{27}}{{64}}$
$\Rightarrow \tan \theta = {\left( {\dfrac{{27}}{{64}}} \right)^{\dfrac{1}{3}}} = \dfrac{3}{4}$

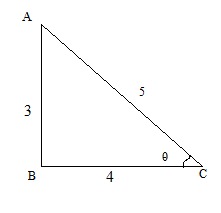
From the above figure, we can say that:
$\sin \theta = \dfrac{3}{5}$ and $\cos \theta = \dfrac{4}{5}$ .
Therefore, the length of log = OA + OD = $\dfrac{{27}}{{\sin \theta }}$+$\dfrac{{64}}{{\cos \theta }}$=$\dfrac{{27}}{{\dfrac{3}{5}}}$m+$\dfrac{{64}}{{\dfrac{4}{5}}}$m= 125m
So, option B is the correct one.

Note- We should find the trigonometric ratio in a right triangle. The relation between the trigonometric function and sides of a right triangle is given as:
$\sin \theta = \dfrac{{{\text{perpendicular}}}}{{hypotenuse}},\cos \theta = \dfrac{{{\text{Base}}}}{{hypotenuse}},\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{Base}}}}$ . Before solving this question, you should also know how to find the maximum and minimum value of a function.