Question

A chain of mass m and length l lies on the surface of a rough sphere of radius R (>l) such that one end of the chain is at the top most point of the sphere. The chain is held at rest because of friction. What is the gravitational potential energy of the chain?

Answer 1

In order to solve this question, we will first the free body diagram of given system and then we will take elementary part of chain and solve for potential energy due to this elementary portion of chain and then using integration rules we will solve for whole mass and length of chain for potential energy.
The gravitational potential energy of mass m and at a height of h is calculated as $U = mgh$ where g is acceleration due to gravity.

Complete answer:
Let us first draw the diagram showing a chain lies on a sphere of radius R. C be the top point on the sphere and at point D, the chain's end point lies. O is the centre of the sphere and consider an elementary portion of chain of length dl is at a height of h from centre O, making an angle of $\theta$ with radius as shown in the diagram as.

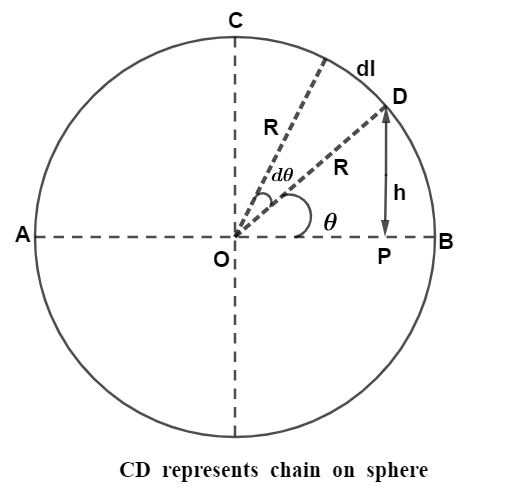
Now, From right angle triangle OPD we see that,
$\sin \theta = \dfrac{{DP}}{{OD}}$ since, $DP = h,OD = R$ so,
$\sin \theta = \dfrac{h}{R}$
$h = R\sin \theta \to (i)$
From the elementary portion of length in the diagram we see that,
$d\theta = \dfrac{{dl}}{R}$ and mass of elementary portion let’s say dm will be
$dm = \dfrac{m}{l}dl$ on putting of value dl, we get,
$dm = \dfrac{m}{l}Rd\theta$
Now, potential energy of this elementary portion let’s say dU will be
$dU = dm(g)h$
$dU = \dfrac{{mRgh}}{l}d\theta$
put the value of h from equation (i) we get,
$dU = \dfrac{{m{R^2}gh}}{l}\sin \theta d\theta$
Now, for complete potential energy of the chain, we need to integrate it from the range of $\theta = \theta \to \theta = \dfrac{\pi }{2}$ so, integrating the equation $dU = \dfrac{{m{R^2}gh}}{l}\sin \theta d\theta$ we get,
$\int {dU} = \dfrac{{m{R^2}gh}}{l}\int\limits_\theta ^{\dfrac{\pi }{2}} {\sin \theta d\theta }$
using integration rules as, $\int {\sin \theta d\theta = - \cos \theta }$
$U = \dfrac{{m{R^2}gh}}{l}[ - \cos \theta ]_\theta ^{\dfrac{\pi }{2}}$
$U = \dfrac{{m{R^2}gh}}{l}[ - \cos \dfrac{\pi }{2} + \cos \theta ]$ and $\cos \dfrac{\pi }{2} = 0$
on putting the values we get,
$U = \dfrac{{m{R^2}gh}}{l}[\cos (\dfrac{\pi }{2} - \dfrac{l}{R})]$ since $\theta = \dfrac{\pi }{2} - \dfrac{l}{R}$
$U = \dfrac{{m{R^2}gh}}{l}[\sin (\dfrac{l}{R})]$
Hence, the gravitational potential energy of the chain is $U = \dfrac{{m{R^2}gh}}{l}[\sin (\dfrac{l}{R})]$ .

Note:
It should be remembered that the relation between angle, length of an arc and radius of a circle is as $\theta = \dfrac{{arc}}{{radius}}$ here angle is always measured in radians. While solving such questions, always check the initial and final limits of integration and remember all the basic integration formulas.