Question

A chain of length L starts sliding down from the horizontal surface of a table. If the hanging length is l, the coefficient of friction between the table and chain is:

A. $\dfrac{l}{L}$
B. $\dfrac{L}{l}$
C. $\dfrac{l}{L-l}$
D. $\dfrac{L-l}{l}$

Answer 1

IN this question we have been given that a chain of length L starts sliding down the horizontal surface. We have been asked to calculate the coefficient of friction between the table and chain. Static friction is the limiting frictional force above which the object starts to slide or move on a surface. We know that the maximum static friction will be equal to the weight of the hanging chain. Since the weight of the hanging chain is the force that is opposed by the static friction.

Complete step by step solution:
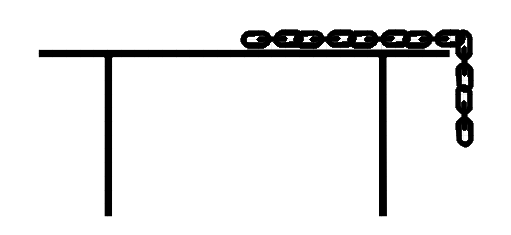
The total length of the chain is given as L, the length of the chain hanging from the table is given as l as shown in the figure.
Let us assume that the chain has a uniformly distributed mass, say ‘m’. Also, the length of chain on the table will be (L-l).
Therefore,
mass of chain on the table $=\dfrac{mg(L-l)}{L}$
Similarly,
mass of chain hanging from the table $=\dfrac{mgl}{L}$
Now, we know that
$F=\mu N$ ……………… (1)
Where, F is the frictional force, N is the normal reaction and $\mu$is the coefficient of friction.
We know that
$N=\dfrac{mg(L-l)}{L}$ ………………… (2)
We also know that, the maximum frictional force is equal to the weight of the hanging chain
Therefore,
$F=\dfrac{mgl}{L}$ ………………….. (3)
Therefore, from (1), (2) and (3)
We get,
$\dfrac{mgl}{L}=\mu \dfrac{mg(L-l)}{L}$
On solving,
We get,
$\mu =\dfrac{l}{(L-l)}$

So, the correct answer is “Option C”.

Note: When we try to move an object, we experience a friction force. This force is known as static friction force. The static friction force keeps the object at rest. Therefore, it opposes motion. The friction force experienced when on a moving object is known as dynamic friction force. This force acts opposite to the direction of the motion of the object.