Question

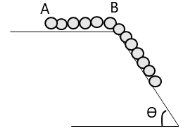
A chain of length $L$ and mass $m$ is placed upon a smooth surface. The length of BA is $\left( {L - b} \right)$. Calculate the velocity of the chain when its end reaches B.

A. $\sqrt {\dfrac{{2g\sin \theta }}{L}\left( {{L^2} - {b^2}} \right)}$
B. $2\sqrt {\dfrac{{g\sin \theta }}{L}\left( {{L^2} - {b^2}} \right)}$
C. $\sqrt {\dfrac{{g\sin \theta }}{L}\left( {{L^2} - {b^2}} \right)}$
D. $\sqrt {\dfrac{{g\sin \theta }}{{2L}}\left( {{L^2} - {b^2}} \right)}$

Answer 1

Use the formulae for potential energy and kinetic energy of the object. When the end of the chain reaches the point B, the potential energy lost by the chain is equal to the gain in kinetic energy of the chain. Determine the values of initial and final potential energies of the chain and gain in kinetic energy of chain and determine the required velocity.

Formulae used:
The potential energy $U$ of an object is
$U = mgh$ …… (1)
Here, $m$ is the mass of the object, $g$ is acceleration due to gravity and $h$ is the perpendicular distance of the object from ground.
The kinetic energy $K$ of an object is
$K = \dfrac{1}{2}m{v^2}$ …… (2)
Here, $m$ is the mass of the object and $v$ is the velocity of the object.

Complete step by step answer:
We have given that the mass of the chain is $m$ and the length of the chain is $L$. The length of the segment BA of the chain is $\left( {L - b} \right)$. Hence, the length of the remaining portion of the chain will be $b$.
The initial and final position of the chain is as shown in the following diagram:

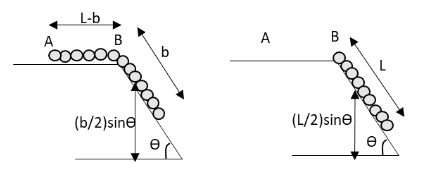
The initial potential energy ${U_i}$ of the chain is
${U_i} = \left( {\dfrac{m}{L}b} \right)g\dfrac{b}{2}\sin \theta$
$\Rightarrow {U_i} = \dfrac{{m{b^2}g\sin \theta }}{{2L}}$
Here, $\dfrac{m}{L}b$ is the mass of the length of the chain on the inclined plane
The final potential energy of the chain is
${U_f} = mg\dfrac{L}{2}\sin \theta$
Here, ${h_f}$ is the height of the centre of mass of the chain when its whole length is on the inclined plane.
According to law of conservation of energy, when the left end of the chain reaches point B, the potential energy possessed by the chain is lost and converted into kinetic energy of the chain.
${U_f} - {U _i} = K$
Substitute $mg\dfrac{L}{2}\sin \theta$ for ${U_f}$, $\dfrac{{m{b^2}g\sin \theta }}{{2L}}$ for ${U _i}$ and for $K$ in the above equation.
$mg\dfrac{L}{2}\sin \theta - \dfrac{{m{b^2}g\sin \theta }}{{2L}} = \dfrac{1}{2}m{v^2}$
Here, $v$ is the velocity of the chain when its end reaches point B.
$\dfrac{{g{L^2}\sin \theta - {b^2}g\sin \theta }}{{2L}} = \dfrac{1}{2}{v^2}$
$\Rightarrow \dfrac{{g{L^2}\sin \theta - {b^2}g\sin \theta }}{L} = {v^2}$
$\therefore v = \sqrt {\dfrac{{g\sin \theta }}{L}\left( {{L^2} - {b^2}} \right)}$
Therefore, the velocity of the chain when its ends reaches point B is $\sqrt {\dfrac{{g\sin \theta }}{L}\left( {{L^2} - {b^2}} \right)}$.

Hence, the correct option is C.

Note: The students should not mistake to calculate the mass of the chain in its initial position. The length of the mass of the inclined plane is the mass per unit total length of the chain multiplied by the length of the chain on the inclined plane. If this value is not taken correctly, the final answer will also be incorrect.