Question: A chain of 5 links each of mass 0.1 kg is lifted vertically with a constant acceleration\(1.2\ ms^{-...

Question

A chain of 5 links each of mass 0.1 kg is lifted vertically with a constant acceleration $1.2\ ms^{-2}$ . The force of intersection between the top link and the one immediately below it is:
A. 5.5 N
B. 4.4 N
C. 3.04 N
D. 7.6 N

Answer 1

Solution

The acceleration of the chain confirms that there is a force acting on the chain so that it can move upward. These types of questions can be easily solved by drawing the free body diagram of the chain and analyzing different parts of the chain between which the value of force is required. Using a free body diagram, we can find the acceleration of the system and then proceed by finding other parameters.

Formula used:
Formula used: $\sum F_{net} = m\times a_{com}$

Complete step by step answer:
Let’s first draw the free body diagram of the chain.

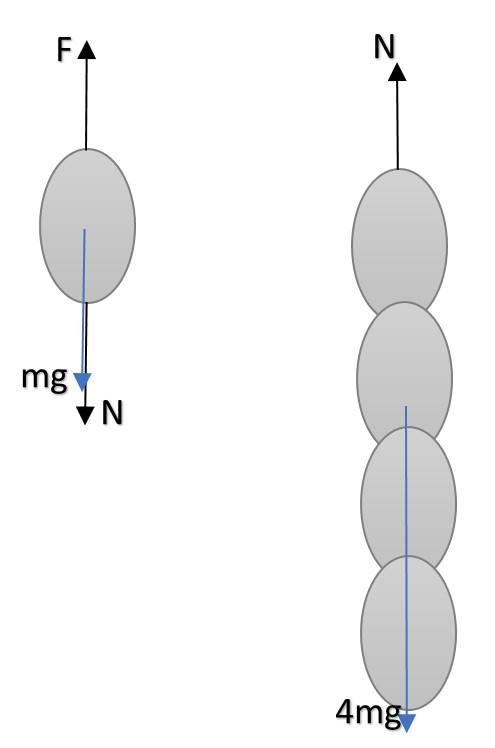
Let the force applied by the external agent be ‘F’ and the force between the required links be ‘N’. Let the mass on one link be ‘m’ so the rest of the mass will be ‘4m’.
Now, we know the acceleration of both parts of chain, hence writing force equation for bigger part of chain, we get:
$\sum F_{net} = m\times a_{com}$
$N - 4mg = 4m\times a$
Hence $N = 4m(a+g) = 4\times 0.1 \times (1.2 + 9.8) = 4.4 N$
Hence the force between the $1^{st}$ and rest of the links is 4.4N, option B. is correct.

Additional information:
Mostly, we can take the value of $g=10\ ms^{-2}$ for simpler calculations. But one should make sure that it makes the calculations simpler. But in questions such as this, taking $g= 9.8\ ms^{-2}$ would make calculations simpler. In a nut-shell, take the value of ‘g’ so that the calculation becomes simple, unless the value is specified in the question.

Note:
One can also proceed by writing a force equation for a smaller part of the chain. But it will have one more unknown ‘F’. In order to find this unknown, we have to write the force equation on the whole chain, assuming it to be a single object. But since we have the acceleration of all parts of the chain, hence we can directly write the equation on the part having the least number of variables.