Question

A chain is held on a frictionless horizontal table with one-fourth of its length hanging over the edge. If the chain has length l and mass M, what is the work required to pull the hanging part back on the table?

Answer 1

Since the part of the chain is hanging around the table, the work done on bringing up the hanging part of the chain will be equal to the product of the weight exerted by the hanging portion of the chain and the distance to which the chain has to be pulled upwards.

Complete step by step answer:
Consider the chain hanging from a frictionless table, such that only one-fourth of the total length $l$ of it is hanging down the table.

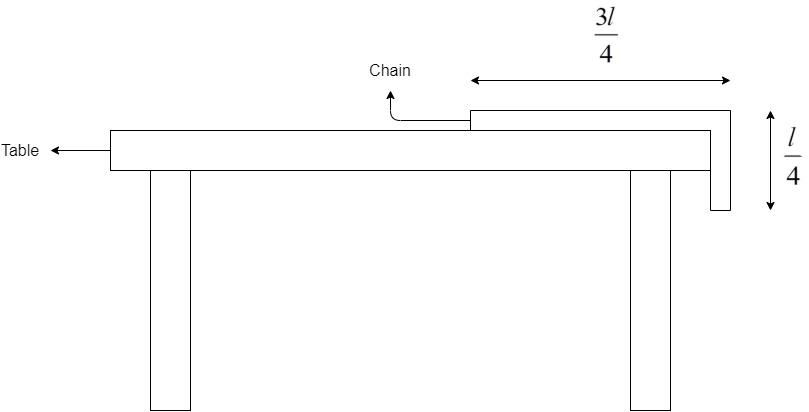
Assuming that the distribution of mass in the chain is constant throughout the chain, we can say that the portion of the chain of mass m hanging from the table has the mass equal to $\dfrac{m}{4}$ as shown below

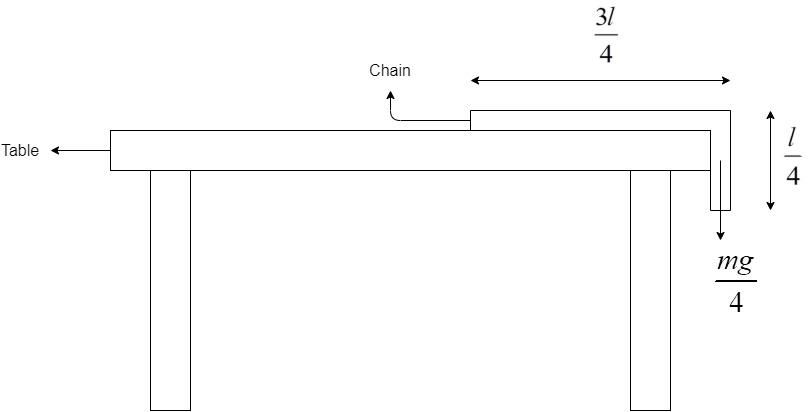
This portion of mass exerts weight in the downward direction equal to,
Weight of the entire chain, $F = mg$
Weight of the hanging portion,
$\Rightarrow F = \dfrac{m}{4}g = \dfrac{{mg}}{4}$
The work done is moving the hanging portion of the chain up,
$W = F \times S$
where S is the distance to be moved and F is the weight exerted by the hanging portion.
Here, the weight of the hanging portion acts on the centroid of the hanging portion which is nothing but the center of the hanging portion.
Length of the hanging portion is $\dfrac{l}{4}$
$\therefore S = \dfrac{{\dfrac{l}{4}}}{2} = \dfrac{l}{8}$
Substituting in the above equation of work done,
$W = F \times S$
$\Rightarrow W = \dfrac{{mg}}{4} \times \dfrac{l}{8}$
$\Rightarrow W = \dfrac{{mgl}}{{32}}$

Therefore, the work done in lifting the hanging portion, $W = \dfrac{1}{{32}}mgl$.

Note:
In this problem, it is mentioned as a frictionless tabletop surface. If there is friction present, then,
The coefficient of friction would be given as $\mu$.
Then, the weight F to be considered in the equation of work above, should be considered as:
$\Rightarrow F = \dfrac{{mg}}{4} - \mu \dfrac{{mg}}{4} = \dfrac{{mg}}{4}\left( {1 - \mu } \right)$
This value of the force should be substituted in the equation of the work.