Question
Question: A chain consisting of 5 links each of mass 0.1 kg is lifted vertically up with a constant accelerati...
A chain consisting of 5 links each of mass 0.1 kg is lifted vertically up with a constant acceleration of 2.5 m/s2. The force of interaction between 1st and 2nd links as shown
A. 5.20 N
B. 4.92 N
C. 9.84 N
D. 2.46 N
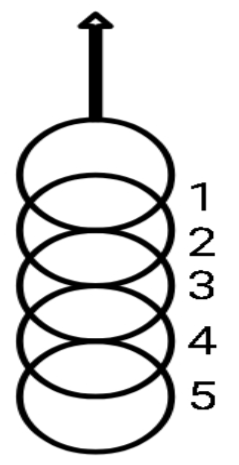
Solution
A force of tension will act between link 1 and 2. The weight below the link one will be responsible for the tension that link 1 will experience. When a body is accelerated in the upward direction, it’s weight increases.
Formula used:
The apparent weight of anybody accelerating up with ‘a’ acceleration is given as:
W = m(g+a).
Complete step-by-step solution:
We are given that the links are accelerating upwards.
Consider the elevator problem. When an elevator accelerates upwards we know that the apparent weight of the body in it increases. If the body has no acceleration, it's weight is mg. When the body is undergoing acceleration a in the upwards direction, and we measure it by a weighing machine, it's weight will be:
W = m(g+a).
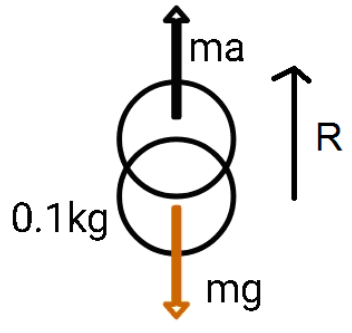
Now, consider if the problem to be consisting of only link 1 and link 2. On link 2, we can see two forces acting, one ma upwards, and other mg downwards. Therefore, as we balance these forces, we find the reaction force as:
ma=R−mg
(as we consider the up arrow to be positive).
This reaction is nothing but the apparent weight of the link (2).
Therefore, we will observe that when the links are accelerating upward then their apparent weight will be:
R=ma+mg ⇒W=m(a+g)
⇒W=0.1×(9.8+2.5)N
⇒W=1.23N.
Now, the force of interaction between link 1 and link 2 will be purely due to their weights. The apparent weight of 4 chains below the link 1 will exert a tension between link 1 and 2, which will have a magnitude equal to 4 times the apparent weight of a link that we just calculated. So we can write:
Total weight = 4×1.23 N = 4.92 N.
Therefore the correct answer is an option (B). The force of interaction between the 1st and 2nd links is just 4.92 N.
Note: To remember the results of the elevator problem better one can just simply remember the weightlessness condition. When a body is freely falling, its acceleration is downwards and is equal to g which makes the apparent weight of the body to be zero. Therefore when the acceleration in our case was upwards we had to add that acceleration to find out the apparent weight.
