Question

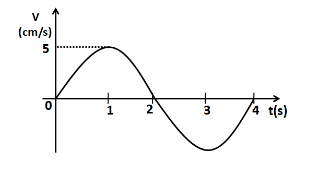
A certain transverse sinusoidal wave if wavelength $20vm$ is moving in the positive x-direction. The transverse velocity of the particle at $x = 0$ as a function of time is shown. The amplitude of the motion is

(A) $\dfrac{5}{\pi }cm$
(B) $\dfrac{\pi }{2}cm$
(C) $\dfrac{{10}}{\pi }cm$
(D) $2\pi cm$

Answer 1

To solve this question, we have to differentiate the general equation of wave with respect to time to get the expression for the velocity amplitude. Then we have to find out the values of the angular frequency and the velocity amplitude from the given graph. Substituting these values in the expression for the velocity amplitude, we will get the required value of the amplitude of the motion.

Formula used: The formula used to solve this question is given by
$f = \dfrac{1}{T}$ , here $f$ is the frequency, and $T$ is the time period.
$\omega = 2\pi f$ , here $\omega$ is the angular frequency, and $f$ is the frequency.

Complete step-by-step solution:
Let the amplitude of the motion of the given transverse wave be $A$ . Also, let $\omega$ be its angular frequency, and $k$ be its wave number.
Since the wave is sinusoidal, so we can assume the equation of the given transverse wave in space and time coordinates as
$y\left( {x,t} \right) = A\sin \left( {\omega t - kx + \varphi } \right)$ .............................(1)
Now, we know that the transverse velocity of the particles is given by
$v = \dfrac{{\delta y}}{{\delta t}}$
Therefore, we differentiate (1) partially with respect to the time $t$ on both the sides to get
$v\left( {x,t} \right) = \omega A\cos \left( {\omega t - kx + \varphi } \right)$
According to the question, we have $x = 0$ . Substituting this above, we get
$v\left( {x,t} \right) = \omega A\cos \left( {\omega t + \varphi } \right)$ .............................(2)
From the above relation, we can observe that the amplitude of the transverse velocity of the particle is equal to $\omega A$ . From the given graph, we can easily observe that the amplitude of the transverse velocity of the particle is equal to $5cm/s$ . So we can say that
$\omega A = 5$ .............................(3)
From the given graph we can also observe that one cycle of the transverse velocity is being completed in $4s$ . So the time period of the given transverse wave can be written as
$T = 4s$ .............................(4)
Now, we know that the frequency is related to the time period by the relation
$f = \dfrac{1}{T}$
Putting (4) in the above equation, we get
$f = \dfrac{1}{4}Hz$
Now, the angular frequency is given by
$\omega = 2\pi f$
$\Rightarrow \omega = 2\pi \left( {\dfrac{1}{4}} \right)$
On solving we get
$\omega = \dfrac{\pi }{2}rad/s$ .............................(5)
Putting (5) in (3) we have
$A\left( {\dfrac{\pi }{2}} \right) = 5$
$\Rightarrow A = \dfrac{{10}}{\pi }cm$
Thus, the amplitude of the motion is equal to $\dfrac{{10}}{\pi }cm$ .
Hence, the correct answer is option C.

Note
Do not be confused between particle velocity and the wave velocity. The particle velocity is the velocity of the particles of the mediums in which the wave is propagating. But the wave velocity is the velocity of a crest, a trough, or any point on the wave.