Solveeit Logo
Login

Question

Question: A certain mass of an ideal gas is at pressure \[{P_1}\] and volume \[{V_1}\]​. It is compressed isot...

A certain mass of an ideal gas is at pressure P1{P_1} and volume V1{V_1}​. It is compressed isothermally and then allowed to expand adiabatically until its pressure returns to P1{P_1}. The gas is then allowed to expand its original volume. Which of the following P-V graphs represents the process correctly?
A.
B.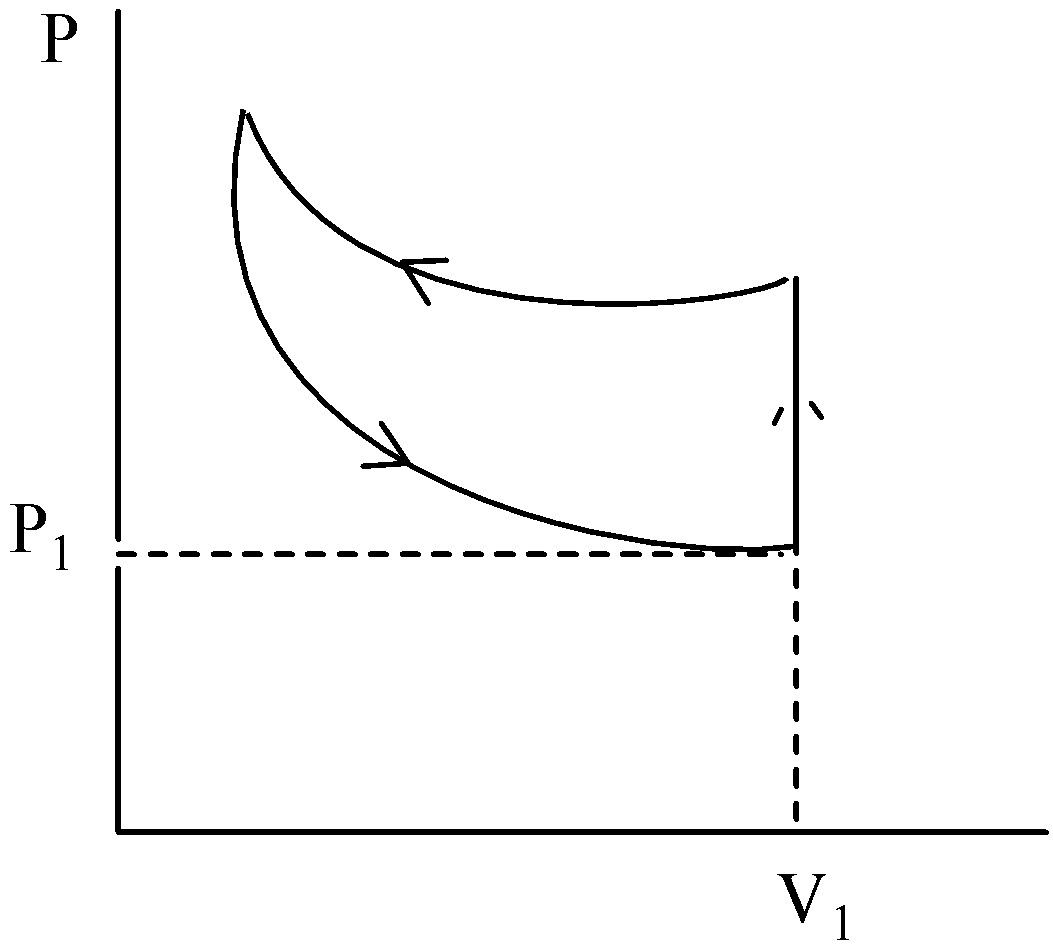
C.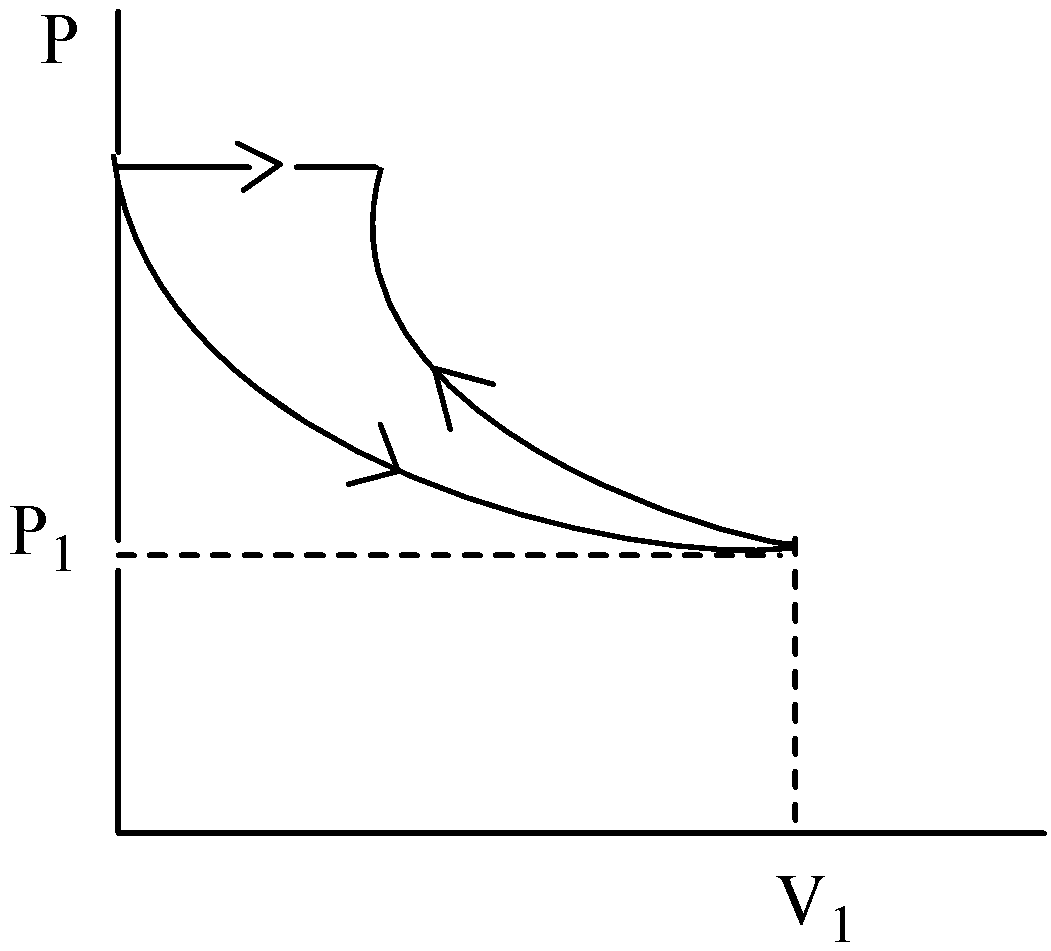
D.

Explanation

Solution

We need to know that in the case of ideal gas, there are so many randomly moving point particles and it is not undergoing any interparticle interactions. And the ideal gases should obey the ideal gas law and it follows some rules. That is, the molecules present in the ideal gas, which does not attract or repels each other. And there is only an elastic collision between the ideal gas molecules.

Complete answer:
In the case of an isothermal process,
PV=PV = Constant
Pdv=−dPVPdv = - dPV
By rearranging the equation,
dPdV=−PV\dfrac{{dP}}{{dV}} = - \dfrac{P}{V}
For the adiabatic process,
PVγ=P{V^\gamma } = Constant
dPdV=−γPV\dfrac{{dP}}{{dV}} = - \gamma \dfrac{P}{V}
A certain mass of an ideal gas is at pressure P1{P_1} and volume V1{V_1}​, It is compressed isothermally. Then the pressure increases and volume decreases with hyperbola. And until the pressure comes back to P1{P_1}, the gas will expand adiabatically. Then the graph will be a slightly steeper hyperbola than the graph of hyperbola.
The gas is permitted to expand its original volume which is represented in a graph by a straight line.

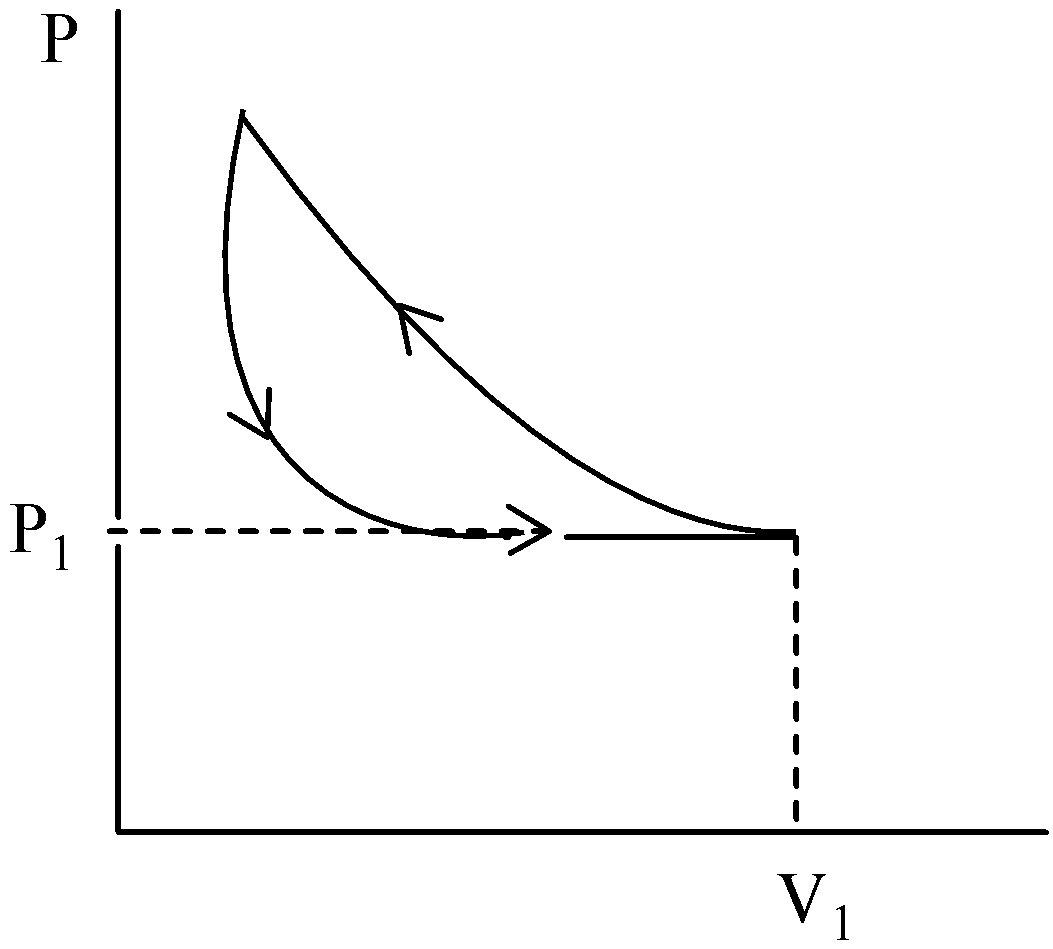
Hence, option (A) is correct.
This is not the correct graphical representation of this process. Hence, the option (B) is incorrect.
The representation of the P- V graph of the given process is not plotted correctly. Hence, option (C) is incorrect.
This is not the correct graphical representation of the P- V graph of the given process. Hence, the option (D) is incorrect.

Hence, option (A) is correct.

Note:
In the case of isothermal reversible expansion, the volume is slowly increasing in the presence of a constant temperature. In the case of an isothermal reversible expansion process, the expansion of PV work done was possible by the absorption of heat reversibly into the ideal gas. And they do not lose the heat. But the change in internal energy will be equal to zero.