Question

A certain current liberates 0.500g of H₂ in 2.00hr. How many gram of oxygen can be liberated by the same current in the same time?

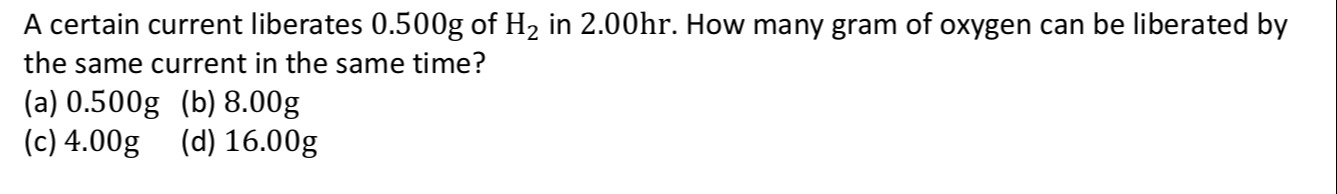
• A. 0.500g
• B. 8.00g
• C. 4.00g
• D. 16.00g

Answer 1

Answer: (C)

4.00g

Answer 2

The problem involves the electrolysis of water, where hydrogen gas is liberated at the cathode and oxygen gas is liberated at the anode. We are given the mass of hydrogen liberated by a certain current in a certain time and asked to find the mass of oxygen liberated by the same current in the same time. This scenario is governed by Faraday's laws of electrolysis, specifically Faraday's second law.

Faraday's second law of electrolysis states that when the same quantity of electricity is passed through different electrolytes, the masses of different substances deposited or liberated at the electrodes are directly proportional to their chemical equivalent weights.

Mathematically, for two substances 1 and 2, if the same quantity of electricity is passed, then:

$$\frac{m_1}{E_1} = \frac{m_2}{E_2}$$

where $m_1$ and $m_2$ are the masses of the substances liberated, and $E_1$ and $E_2$ are their respective chemical equivalent weights.

The electrode reactions for the electrolysis of water are:

At the cathode (reduction): $2H_2O(l) + 2e^- \rightarrow H_2(g) + 2OH^-(aq)$ (or $2H^+(aq) + 2e^- \rightarrow H_2(g)$ in acidic solution)

At the anode (oxidation): $2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4e^-$

To calculate the equivalent weight ($E$) of a substance, we use the formula:

$$E = \frac{\text{Molar mass (M)}}{\text{Number of electrons involved in the reaction per molecule (n)}}$$

For hydrogen ($H_2$):

Molar mass of $H_2$, $M_{H_2} \approx 2.0 \text{ g/mol}$.

From the cathode reaction, 2 electrons are involved in the formation of one molecule of $H_2$. So, $n_{H_2} = 2$.

Equivalent weight of $H_2$, $E_{H_2} = \frac{M_{H_2}}{n_{H_2}} = \frac{2.0 \text{ g/mol}}{2 \text{ eq/mol}} = 1.0 \text{ g/eq}$.

For oxygen ($O_2$):

Molar mass of $O_2$, $M_{O_2} \approx 32.0 \text{ g/mol}$.

From the anode reaction, 4 electrons are involved in the formation of one molecule of $O_2$. So, $n_{O_2} = 4$.

Equivalent weight of $O_2$, $E_{O_2} = \frac{M_{O_2}}{n_{O_2}} = \frac{32.0 \text{ g/mol}}{4 \text{ eq/mol}} = 8.0 \text{ g/eq}$.

We are given the mass of hydrogen liberated, $m_{H_2} = 0.500$ g. We need to find the mass of oxygen liberated, $m_{O_2}$. Since the same current flows for the same time, the quantity of electricity passed is the same for both processes. Applying Faraday's second law:

$$\frac{m_{H_2}}{E_{H_2}} = \frac{m_{O_2}}{E_{O_2}}$$

Substitute the known values:

$$\frac{0.500 \text{ g}}{1.0 \text{ g/eq}} = \frac{m_{O_2}}{8.0 \text{ g/eq}}$$

Now, solve for $m_{O_2}$:

$$m_{O_2} = 0.500 \text{ g} \times \frac{8.0 \text{ g/eq}}{1.0 \text{ g/eq}}$$ $$m_{O_2} = 0.500 \times 8.0 \text{ g}$$ $$m_{O_2} = 4.00 \text{ g}$$

Thus, 4.00 grams of oxygen can be liberated by the same current in the same time.