Question

A Cassegrain telescope uses two mirrors as shown in Fig. 9.26. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?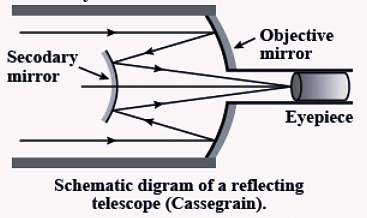Fig. 9.26

Answer 1

The following figure shows a Cassegrain telescope consisting of a concave mirror and a convex mirror.
Distance between the objective mirror and the secondary mirror, d = 20 mm
Radius of curvature of the objective mirror, R1 = 220 mm
Hence, focal length of the objective mirror, $ƒ_1 = \frac{R_1 }{ 2} = 110mm$
Radius of curvature of the secondary mirror, R1 = 140mm
Hence, focal length of the secondary mirror, $ƒ_2 = \frac{R_2 }{2} = \frac{140 }{ 2} = 70mm$
The image of an object placed at infinity, formed by the objective mirror, will act as a virtual object for the secondary mirror.
Hence, the virtual object distance for the secondary mirror, $u = ƒ_1 - d = 110 - 20 = 90mm$
Applying the mirror formula for the secondary mirror, we can calculate image distance (v),
$\frac{1 }{ v} + \frac{1 }{ u} = \frac{1 }{ ƒ_2}$

$\frac{1 }{ v} = \frac{1 }{ ƒ_2} - \frac{1 }{ u}$

$\frac{1 }{ v}= \frac{1 }{ 70} - \frac{1 }{ 90}$

$\frac{1 }{ v}= \frac{9 - 7 }{ 630}$

$\frac{1 }{ v}= \frac{2 }{ 630}$

$v= \frac{630 }{ 2}$
$v= 315$ mm

Hence, the final image will be formed 315 mm away from the secondary mirror.