Question
Question: A cart of mass M has a pole on it from which a ball of mass \(\mu\) hangs from a thin string attache...
A cart of mass M has a pole on it from which a ball of mass μ hangs from a thin string attached to point P. The cart and the ball have initial velocity v. The cart crashes onto another cart of mass m and sticks to it. The length of the string is R. If the smallest initial velocity from which the ball can go in the circle around point P is v, find the value of v. (Neglect friction and take M,m>>μ)
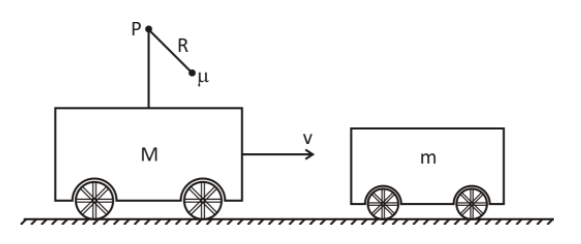
A.(MM+m)4gR
B.(mM+m)4gR
C.(mM+m)5gR
D.(MM+m)5gR
Solution
The problem can be solved using law of conservation of momentum. According to which in the absence of any external force, the total momentum of any object or system is conserved or remains constant.
Complete step by step solution:
Mass of ball = μ
Initial velocity of the cart and the ball =v
Mass of another cart = m
The length of the string =R.
Friction is negligible.
Mass of another cart = m⟩ Mass of ball = μ
The law of conservation of momentum states “In the absence of any external force, the total momentum of any object or system is conserved or remains constant.”
Mv=(M+m)v’
Where v′= velocity of the two carts after collision.
∴v′=(M+m)Mv
Consider the circular motion of the ball atop the cart if it were stationery. If at the lowest and highest points the ball has speeds arev1 and v2 respectively, then according to law of conservation of energy the total energy of an isolated system remains constant.
Hence
21×μv12+21×μv22=2μgR
⇒Rμv22=T+μg
Where g= acceleration due to gravity
And T= the tension in the string when the ball is at the highest point
The smallestv1is given as -T=0
And the smallestv2is given as-
21×μv12=2μgR+21×μgR
⇒μv12=4μgR+μgR
⇒μv12=5μgR
⇒v12=5gR
⇒v1=5gR
As the ball has initial velocity, velocity of the ball relative to the cart after the collision=v−v′
Hence, the smallest velocity for the ball to go round in a circle after the collision is given by-
v1=v−v′
⇒v1= v−(M+m)Mv
⇒5gR=v−(M+m)Mv
⇒v=(mM+m)5gR
Hence, option (C) is the correct answer.
Note: In physics, conservation law states that a particular measurable property of an isolated physical system does not change with time. These conservation laws include- Conservation of energy, Conservation of linear momentum, Conservation of linear momentum, Conservation of angular momentum etc.
In this particular question, we have used conservation of linear momentum which states that in the absence of any external force, the total momentum of any object or system is conserved. Additionally according to the law of conservation of energy, it can neither be created nor be destroyed only its form can be changed from one to another.
