Question

A cart of mass $20\,{\text{kg}}$ at rest is to be dragged at a speed of $18\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$. If the coefficient of friction between the cart and the ground is 0.1, what is the minimum force required to drag the cart to a distance of $10\,{\text{m}}$? (Take $g = 10\,{\text{m/}}{{\text{s}}^2}$)

Answer 1

Determine the acceleration of the cart during its travel using a third kinematic equation. Apply Newton’s second law of motion to the cart in the vertical and horizontal direction. First determine the value of the normal force and then substitute its value in the formula for frictional force. Hence, determine the force required to drag the cart.

Complete step by step answer:
The expression for Newton’s second law of motion is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.
The third kinematic equation is given by
${v^2} = {u^2} + 2as$ …… (2)
Here, $v$ is final velocity of the object, $u$ is initial velocity of the object, $a$ is acceleration of the object and $s$ is displacement of the object.
The frictional force ${F_f}$ acting on an object is
${F_f} = \mu N$ …… (3)
Here, $\mu$ is the coefficient of friction and $N$ is the normal force acting on the object.

We have given that mass of the cart is $20\,{\text{kg}}$ and it is moving with a speed of $18\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$.
$m = 20\,{\text{kg}}$
$v = 18\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$
Convert the unit of velocity of the cart in the SI system of units.
$v = \left( {18\,\dfrac{{{\text{km}}}}{{\text{h}}}} \right)\left( {\dfrac{{{{10}^3}\,{\text{m}}}}{{1\,{\text{km}}}}} \right)\left( {\dfrac{{1\,{\text{h}}}}{{3600\,{\text{s}}}}} \right)$
$\Rightarrow v = 5\,{\text{m/s}}$
Hence, the velocity of the cart is $5\,{\text{m/s}}$.

Let us first determine the acceleration of the cart during its travel.The cart starts from the rest. Hence, its initial velocity is zero and the final velocity of the cart is $5\,{\text{m/s}}$.
$u = 0\,{\text{m/s}}$
The cart travels a distance of $10\,{\text{m}}$ after applying the force. Hence, the displacement of the car is $10\,{\text{m}}$.
$s = 10\,{\text{m}}$
Substitute $5\,{\text{m/s}}$ for $v$, $0\,{\text{m/s}}$ for $u$ and $10\,{\text{m}}$ for $s$ in equation (2).
${\left( {5\,{\text{m/s}}} \right)^2} = {\left( {0\,{\text{m/s}}} \right)^2} + 2a\left( {10\,{\text{m}}} \right)$
$\Rightarrow 20a = 25$
$\Rightarrow a = \dfrac{{25}}{{20}}$
$\Rightarrow a = 1.25\,{\text{m/}}{{\text{s}}^2}$
Hence, the acceleration of the cart is $1.25\,{\text{m/}}{{\text{s}}^2}$.

Draw the free body diagram of the cart.

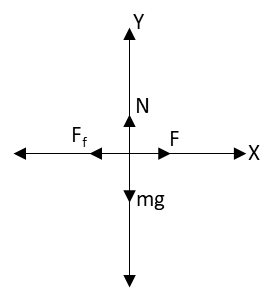
In the above free body diagram, $mg$ is the weight of the cart, $N$ is the normal force acting on the cart, ${F_f}$ is the frictional force on the cart and $F$ is the force required to frag the cart.Apply Newton’s second law of motion to the cart in the vertical direction.
$N = mg$
Apply Newton’s second law of motion to the cart in the vertical direction.
$F - {F_f} = ma$
Substitute $\mu N$ for ${F_f}$ in the above equation.
$F - \mu N = ma$
Substitute $mg$ for $N$ in the above equation.
$F - \mu mg = ma$
$\Rightarrow F = m\left( {a + \mu g} \right)$

Substitute $20\,{\text{kg}}$ for $m$, $1.25\,{\text{m/}}{{\text{s}}^2}$ for $a$, $0.1$ for $\mu$ and $10\,{\text{m/}}{{\text{s}}^2}$ for $g$ in the above equation.
$\Rightarrow F = \left( {20\,{\text{kg}}} \right)\left[ {\left( {1.25\,{\text{m/}}{{\text{s}}^2}} \right) + \left( {0.1} \right)\left( {10\,{\text{m/}}{{\text{s}}^2}} \right)} \right]$
$\Rightarrow F = 20\left[ {1.25 + 1} \right]$
$\Rightarrow F = 20\left( {2.25} \right)$
$\therefore F = 45\,{\text{N}}$

Hence, the minimum force required to drag the cart is $45\,{\text{N}}$.

Note:
One can also solve the same question by another method. One can determine the total kinetic energy of the cart using given velocity and mass of cart. Then the force required to drag the cart can be determined by taking the sum of the work due to frictional force and work due to drag force and equating it to the kinetic energy of the cart.