Question

A cart is moving horizontally along a straight line with constant speed 30m/s. A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved 80m. At what speed (relative to the cart in m/s) must the projectile be fired? (g= $10m{s^{ - 2}}$).
A. 10
B. $10\sqrt 8$
C. $\dfrac{{40}}{3}$
D. None of these

Answer 1

Hint: There are two components of the motion of the particle. A horizontal motion because it is fired from a horizontally moving cart and vertical motion as it is fired upwards relative to the cart. Use kinematic equations of motion of particles by substituting time required by the cart to move 80m. The particle should also take the same time to return back to the same point.

Complete answer:

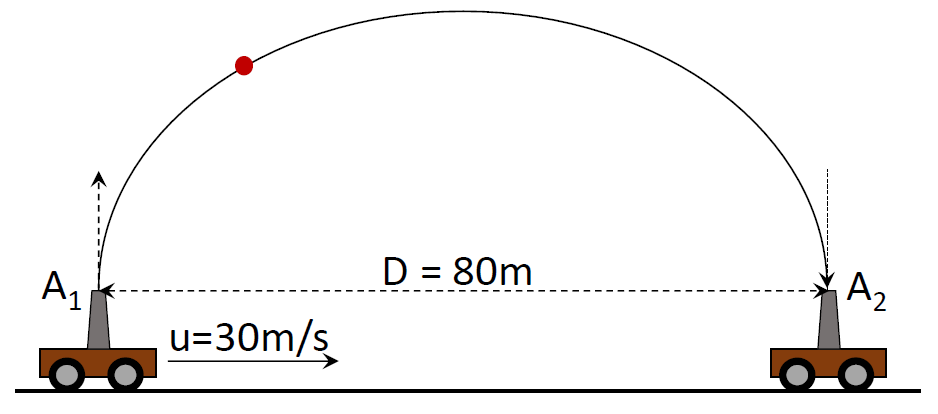
As shown in the above diagram, let the particle be fired in the upward direction at point A1 and return back to the firing point while the cart has moved to A2, covering a distance, $D = 80m$. The speed of the cart during this motion is a constant, $u = 30m/s$. Since speed = distance/time, we can calculate the time taken to cover above distance as $t = \dfrac{D}{u} = \dfrac{{80}}{{30}} = \dfrac{8}{3}s$.
For the particle to return back to the same point of cart, the particle should take the same time as calculated above. Figure shows a rough trajectory of the particle. Now the particle is fired in a vertical direction relative to the cart. Thus the particle will have two components of motion. First one can be considered as the horizontal motion travelled with the same velocity as the cart. Second one is the vertical direction relative to the cart under the effect of acceleration due to gravity. This motion is also called the projectile motion. In the above calculated time, the particle will have to reach the highest point and move downwards. Since the particle is moving under the influence of gravity in the vertical direction, its vertical velocity will decrease to zero by the time it reaches the highest point of the trajectory. Its velocity at that point will be purely horizontal.
Let us consider the vertical motion from the point particle is fired and the point it reaches the maximum point. We have to calculate the vertical velocity by which the particle was fired and let it be${v_1}$. As discussed before, its vertical velocity at highest point, ${v_2} = 0m/s$. Time taken to reach the point is half the time taken for the cart to reach from A1 to A2. We can say this because, both the points are at the same horizontal level and the vertical motion is purely motion under gravity which is constant before and after the highest point. We also considered the fact that there are no other forces acting on the particle during its flight. Using the first kinematic equation which is as follows:
${v_2} = {v_1} + a{t_1}$, where $a = - g = - 10m{s^{ - 2}}$and ${t_1} = \dfrac{t}{2} = \dfrac{8}{{2 \times 3}} = \dfrac{4}{3}s$. (Here we consider the conventional sign with upward as positive.). Substituting the values, we get,
$0 = {v_1} - 10 \times \dfrac{4}{3}$
${v_1} = \dfrac{{40}}{3}m/s$
Comparing the final result with the above given choices, we can say that option C is correct.

Note: The particle is shot at a particular height from the ground as shown in the diagram, which does not affect the time and velocity by which it was fired. It will only affect the maximum height the particle reaches relative to the ground. Above exercises are based on ideal motions but in reality other forces will affect the projectile motions, for instance, on windy days, the air will exert drag force on the particle.