Question

A cart having $4$ wheels is drawn with a constant force ${{F}_{0}}=16\text{ N}$ up an inclined plane, making an angle $\alpha =30{}^\circ$ with the horizontal. The platform of the cart weighs ${{W}_{0}}=18\text{ N}$ and each of its uniform wheels (cylindrical) weighs $W=2\text{ N}$. If the initial velocity is zero, the linear velocity ${{v}_{1}}$ (in $m{{s}^{-1}}$) of the cart when it has travelled a distance of $P=4\text{ m}$ is:
(Given: The wheels roll without slipping and neglect rolling friction)

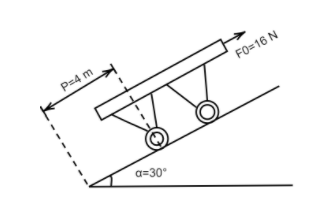
A. $1.4$
B. $2.8$
C. $9.8$
D. $4.2$

Answer 1

To solve this question, we will use the work energy equation. The work done on the system by the force as given in the question makes the cart move up the inclined plane. Work and energy of the system remain conserved if any non-conservative forces do not act on the system. In this case there is no conservative force work done will get converted into some other form to do the required work.

Complete step-by-step answer:
The work done by given force ${{F}_{0}}$ will go away in giving a kinetic energy to the cart and pulling it up by a distance of $P=4\text{ m}$. The kinetic energy of the system i.e., the kinetic energy of the cart and the four wheels that constitute the system will be as follows:
$\begin{aligned} & E={{E}_{platform}}+4{{E}_{wheel}} \\\ & \Rightarrow E=\dfrac{1}{2}{{m}_{platform}}{{v}^{2}}+4\left( \dfrac{1}{2}{{m}_{wheel}}{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}} \right) \\\ & \Rightarrow E=\dfrac{1}{2}{{m}_{platform}}{{v}^{2}}+4\left( \dfrac{1}{2}{{m}_{wheel}}{{v}^{2}}+\dfrac{1}{2}\times \dfrac{{{m}_{wheel}}{{R}^{2}}}{2}\times \dfrac{{{v}^{2}}}{{{R}^{2}}} \right) \\\ & \Rightarrow E=\dfrac{1}{2}{{m}_{platform}}{{v}^{2}}+4\left( \dfrac{1}{2}{{m}_{wheel}}{{v}^{2}}+\dfrac{1}{4}{{m}_{wheel}}{{v}^{2}} \right) \\\ & \Rightarrow E=\dfrac{1}{2}{{m}_{platform}}{{v}^{2}}+4\left( \dfrac{3}{4}{{m}_{wheel}}{{v}^{2}} \right) \\\ & \Rightarrow E=\dfrac{1}{2}\times \dfrac{{{W}_{0}}}{g}\times {{v}^{2}}+\dfrac{3W}{g}\times {{v}^{2}} \\\ & \Rightarrow E=\dfrac{1}{2g}\left( {{W}_{0}}+6W \right){{v}^{2}} \\\ \end{aligned}$
Work done in pulling the cart up by a distance of $P=4\text{ m}$ will be:
$W'=\left( {{W}_{0}}+W \right)\left( P\sin \alpha \right)$
Now, we will add the two values that we received, i.e., the value of work done in pulling the cart up by a distance of $P=4\text{ m}$ and the kinetic energy imparted to the system by the force applied on the body. On writing the work energy equation, we get the following equation:

& {{F}_{0}}\times P=\dfrac{1}{2g}\left( {{W}_{0}}+6W \right){{v}^{2}}+\left( {{W}_{0}}+4W \right)\left( P\sin \alpha \right) \\\ & \Rightarrow \dfrac{1}{2g}\left( {{W}_{0}}+6W \right){{v}^{2}}=\left[ {{F}_{0}}-\left( {{W}_{0}}+4W \right)\sin \alpha \right]P \\\ & \Rightarrow v=\sqrt{\dfrac{2gP\left[ {{F}_{0}}-\left( {{W}_{0}}+4W \right)\sin \alpha \right]}{\left( {{W}_{0}}+6W \right)}} \\\ & \Rightarrow v=\sqrt{\dfrac{2\times 9.8\times 4\left[ 16-\left( 18+4\times 2 \right)\sin 30{}^\circ \right]}{\left( 18+6\times 2 \right)}} \\\ & \Rightarrow {{v}^{2}}=\sqrt{\dfrac{78.4\left[ 16-13 \right]}{30}} \\\ & \Rightarrow v=\sqrt{\dfrac{78.4\times 3}{30}} \\\ & \Rightarrow v=\sqrt{\dfrac{235.2}{30}} \\\ & \Rightarrow v=\sqrt{7.84} \\\ & \therefore v=2.8\text{ m}{{\text{s}}^{-1}} \\\ \end{aligned}$$ **So, the correct answer is “Option B”.** **Note:** We have taken the value of moment of inertia in the solution as $I=\dfrac{m{{R}^{2}}}{2}$ because the wheels are given to be in cylindrical shape. Also, the kinetic energy of one wheel will be multiplied by $4$ to calculate the kinetic energies of all the four wheels that are attached to the cart.