Solveeit Logo
Login

Question

Question: A carnot engine working between \(300K\) and \(600K\) has work output of \(800J\) per cycle. The amo...

A carnot engine working between 300K300K and 600K600K has work output of 800J800J per cycle. The amount of heat energy supplied to the engine from source per cycle will be:
A) 1000J1000J
B) 1600J1600J
C) 1200J1200J
D) 900J900J

Explanation

Solution

To solve this question we have use formula of efficiency of carnot engine which is given by η\eta
η=wQ1=Q1−Q2Q1=T1−T2T1\eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}
Where w⇒w \Rightarrow work done by substance
Q1⇒{Q_1} \Rightarrow Heat taken from source
Q2⇒{Q_2} \Rightarrow Remaining heat given to sink
T1⇒{T_1} \Rightarrow Temperature of source
T2⇒{T_2} \Rightarrow Temperature of sink

Step by step solution:
Step 1
In a carnot engine substance take heat or energy from a source which is at temperature T1{T_1} and change some amount of heat into work ww and remaining heat transfer to sink at temperature T2{T_2} as shown in the diagram.


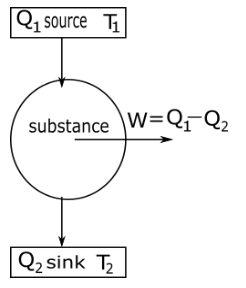
Efficiency of Carnot engine η\eta defined as the ratio of net work done ww by the engine during one cycle to the heat taken in from the source Q1{Q_1} in one cycle thus.
⇒η=wQ1=Q1−Q2Q1\Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}}
The efficiency of the Carnot engine depends on the absolute temperature of the sink and source. So
⇒η=wQ1=Q1−Q2Q1=T1−T2T1\Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}.......... (1)
From this equation
⇒wQ1=T1−T2T1\Rightarrow \dfrac{w}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}
⇒Q1=w(T1T1−T2)\Rightarrow {Q_1} = w\left( {\dfrac{{{T_1}}}{{{T_1} - {T_2}}}} \right)
Step 2
Now we put all given value in this equation
⇒Q1=800(600600−300)\Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{600 - 300}}} \right)
By solving this
⇒Q1=800(600300) ⇒Q1=800(2)  \Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{300}}} \right) \\\ \Rightarrow {Q_1} = 800\left( 2 \right) \\\
∴Q1=1600J\therefore {Q_1} = 1600J
Hence we get the heat given by source is Q1=1600J{Q_1} = 1600J

In this question the option B is correct.

Note:
The efficiency of a Carnot engine is given by ⇒η=wQ1=Q1−Q2Q1=T1−T2T1 \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}} we can find the efficiency of this engine
⇒η=wQ1=8001600=12\Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{800}}{{1600}} = \dfrac{1}{2}
The percentage efficiency of the engine is ⇒η=12×100=50%\Rightarrow \eta = \dfrac{1}{2} \times 100 = 50\%
By this formula we can calculate all values associated with the Carnot engine.