Question

A Carnot engine has the same efficiency between 800K to 500K and xK to 600K. The value of x is:
$\left( a \right)1000K$
$\left( b \right)960K$
$\left( c \right)846K$
$\left( d \right)754K$

Answer 1

We will apply the formula of efficiency of Carnot engine. As there are two different changes in temperature, so we will use the Carnot equation two times by keeping efficiency as equal. After equating two equations the value of x (in Kelvin) temperature will be gained.

Formula used:
$\eta =1-\dfrac{Temp.\,\left( cold \right)}{Temp.\,\left( high \right)}$ where $\eta$ is efficient.

Complete answer:
Carnot engine: It is an engine which is based completely on thoughts rather than on practical basis This is why we can also call it an ideal engine. It is designed in a way that it has a maximum heat efficiency that an engine can bear.

There is also a theorem based on it which is known as Carnot theorem. This theorem is based on the agenda which uses any system in nature with two distinct values of temperature in which one temperature will be higher and the other one will resemble a cold temperature.

Now, we will consider the following diagram to understand the four processes namely, 1 as isothermal expansion, 2 as adiabatic expansion, 3 as isothermal compression and 4 as adiabatic compression.

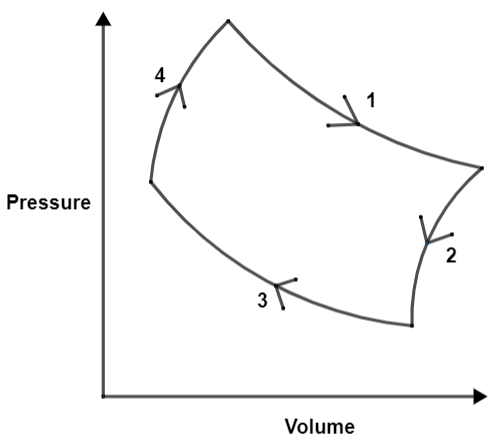
We denote Carnot efficiency by $\eta =1-\dfrac{Temp.\,\left( cold \right)}{Temp.\,\left( high \right)}$. The question describes the same efficiency of the Carnot engine, so initial and final temperatures are going to be equal.

As with same efficiency temperature changes first from 800 K to 500 K so, the equation becomes $\eta =1-\dfrac{500}{800}$…(i)
And again temperature changes from x K to 600 K so, the equation becomes $\eta =1-\dfrac{600}{x}$…(ii)

Now, we will equate equation (i) and (ii), thus we get
$\begin{aligned} & 1-\dfrac{500}{800}=1-\dfrac{600}{x} \\\ & \Rightarrow \dfrac{5}{8}=\dfrac{600}{x} \\\ & \Rightarrow x=\dfrac{600\times 8}{5} \\\ & \Rightarrow x=120\times 8 \\\ & \Rightarrow x=960K \\\ \end{aligned}$

So, the correct answer is “Option B”.

Note:
The higher temperature is basically the description of hot temperature and the cold temperature means cold temperature or low temperature. The high and cold temperatures are basically the temperature provided to the engine and the output of this engine is given cold temperature. This system can never have efficiency greater than the Carnot engine in working position. This is because the Carnot engine is ideal and due to this fact it has excellent efficiency.