Question

A car turns a corner on a slippery road at a constant speed of 10m/s. If the coefficient of friction is 0.5, the minimum radius of the arc in meter in which the car turns is:
A) 20
B) 10
C) 5
D) 4

Answer 1

Here it is given that the car is turning over a corner of a slippery road and we have to find the radius of arc from which the car is turning. So we will first draw a diagram for the given question and see the force which will be applied to the car. By balancing the force we can find the radius of the arc.

Formula used:

& {{F}_{C}}=\dfrac{m{{v}^{2}}}{r} \\\ & f=\mu N \\\ \end{aligned}$$ **Complete answer:** A car is turning with a constant speed of 10m/s forming the arc so the diagram can be given as 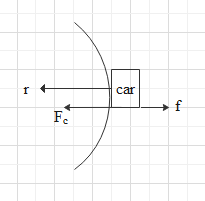 As we can see the car is turning so it will have centripetal force as it is circular motion and this centripetal force $${{F}_{C}}$$ will be balanced here by the frictional force f. If centripetal force is greater than frictional force then the car will slip so the minimum radius will be given when the frictional force is equal to the centripetal force. Now we know that centripetal force is given by $${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}\text{ }..............\text{(i)}$$ Where m is the mass of an object experiencing the force v is the velocity with which the object is moving and r is the radius of the circular path in which the object is moving. And the frictional force is given as the product of coefficient of friction and the normal force. $$f=\mu N\text{ }..............\text{(ii)}$$ Now here the normal force will be balanced by the gravitational force i.e. normal force will be equal to the gravitational force. Hence we can write $$N=mg$$ Here m is the mass and g is acceleration due to gravity. Substituting this value of normal force in equation (ii), we get $$f=\mu mg\text{ }...........\text{(iii)}$$ Now according to the question we have to find the minimum radius of the arc which can be obtained when frictional force is equal to centripetal force. Hence using equation (i) and equation (ii), we get $$\begin{aligned} & \dfrac{m{{v}^{2}}}{r}=\mu mg \\\ & \Rightarrow r=\dfrac{m{{v}^{2}}}{\mu mg} \\\ & \Rightarrow r=\dfrac{{{v}^{2}}}{\mu g} \\\ \end{aligned}$$ We have given the value of v and μ, $$v=10m/s\text{ and }\mu =0.5$$ . The value of acceleration due to gravity is $$g=9.8m/{{s}^{2}}$$. Substituting it in above equation we get $$\begin{aligned} & r=\dfrac{{{10}^{2}}}{\left( 0.5 \right)\left( 9.8 \right)} \\\ & \Rightarrow r=\dfrac{100}{4.9} \\\ & \Rightarrow r=20.4m \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** In case we had taken the value of g as $$10m/{{s}^{2}}$$ then the answer would be exactly 20 meters. Acceleration due to gravity changes with the distance from the equator of the earth and therefore in some numerical it is taken as $$10m/{{s}^{2}}$$. But $$9.8m/{{s}^{2}}$$ is the standard value of g and in the given its value wasn’t provided so we can use either values.