Question

A car travels 5m east in 2 seconds and then halts for the next 3 seconds. The magnitude of displacement of the car at the end of the given time interval is?

Answer 1

- Hint – In this question plot a 4 directional figure, depicting north, west, east and south. Let the motion along the positive x-axis be $\left( {\hat i} \right)$, and form a vector equation to correspond to displacement of the car. This will help getting the answer.

Complete step-by-step solution -

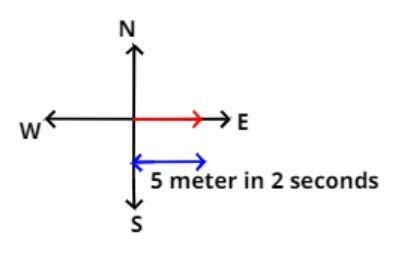
The pictorial representation of the above problem is shown above.
A car travel 5 meter east in 2 seconds and then halts for next 3 seconds (i.e. car does not move for the next 3 seconds)
So the total distance covered is 5 meter in 2 seconds.
And the total time = (2 + 3) seconds
So as the car moves in the east let the direction be $\left( {\hat i} \right)$.
Therefore the distance travelled by the car = $5\hat i$ at the end of a given time interval as it stays for the next 3 seconds at the same position.
So the total displacement (d) of the car is
$d = 5\hat i$ meter.
Now we have to find the magnitude of this so we have to take the modulus so we have,
Magnitude = $\left| d \right| = \left| {5\hat i} \right| = \sqrt {{5^2}} = 5$ meter.
So this is the required answer.

Note – Any vector of the form $a = {a_x}\widehat i + {a_y}\widehat j + {a_z}\widehat k$ has magnitude that is $\left| a \right| = \sqrt {{a_x}^2 + {a_y}^2 + {a_z}^2}$, in other words it is the square root of sum of squares of the individual components of the vector along x, y and z direction. A vector has both direction and magnitude hence the component form depicts the specification of the directions and the magnitude depicts the value.