Question

A car starts from rest and moves with constant acceleration and covers the distance between two points $180m$ apart in $6s$ . its speed as it passes the second point is $45m/s$. Find
(a) Its acceleration
(b) Its speed when it was at the first point
(c) The distance from the first point when it was at rest

Answer 1

The car moves from the rest hence the initial velocity will be zero. The distance between two points and the time taken by the car to cover these points are given. From these data, the equation of the velocity with which the car moves from the $1st$ point can be calculated. Also, the speed when passing the second point is given. From this, the equation of the acceleration will be expressed. Using these equations the values of the required quantities can be found. Also from the values, the required distance will be found by using the equations of motion.

Formula used:
The equations of motion are,
$S = ut + \dfrac{1}{2}a{t^2}$
$\Rightarrow a = \dfrac{{v - u}}{t}$
$\Rightarrow {v^2} = {u^2} - 2as$
Where, $u$ is the initial velocity, $v$ is the final velocity, $S$ is the displacement, $t$ is the required time, $a$ is the acceleration.

Complete step by step answer:
Let us draw a linear diagram,

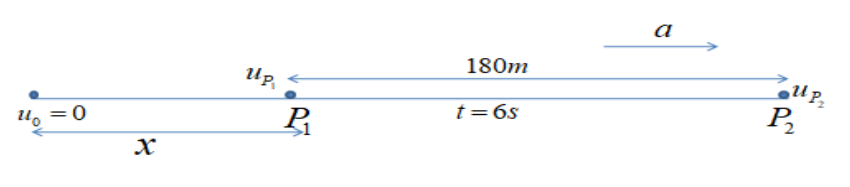
To the acceleration and the speed at the point ${P_1}$ , the equations are
$S = {u_{{P_1}}}t + \dfrac{1}{2}a{t^2}$ ,
Given that,
$S = 180m,t = 6s$
$\Rightarrow 180 = 6{u_{{P_1}}} + \dfrac{{36a}}{2}$
$\Rightarrow 18a + 6{u_{{P_1}}} = 180$
$\Rightarrow 3a = 30 - {u_{{P_1}}}.........(1)$
And, $a = \dfrac{{{u_{{P_2}}} - {u_{{P_1}}}}}{t}$

Given, ${u_{{P_2}}} = 45m/s$
$\Rightarrow a = \dfrac{{45 - {u_{{P_1}}}}}{6}$
$\Rightarrow 3a = \dfrac{{45 - {u_{{P_1}}}}}{2}$
$\Rightarrow 30 - {u_{{P_1}}} = \dfrac{{45 - {u_{{P_1}}}}}{2}$ [ from eq. (1)]
$\Rightarrow 60 - 2{u_{{P_1}}} = 45 - {u_{{P_1}}}$
$\Rightarrow {u_{{P_1}}} = 15m/s.............(2)$
Now, $\Rightarrow a = \dfrac{{45 - {u_{{P_1}}}}}{6}$
$\Rightarrow a = \dfrac{{45 - 15}}{6}$ [from eq. (2)]
$\Rightarrow a = 5\,m/{s^2}.........(3)$

To find the distance between the starting point and the point ${P_1}$, the equation of motion will be
${u_{{P_1}}}^2 = {u_0}^2 - 2ax$
$\Rightarrow {15^2} = {0^2} - 2 \times 5 \times x$[from eq. (2) and (3)]
$\Rightarrow 10x = 225$
$\therefore x = 22.5\,m$

Hence, the answer is:
(a) Its acceleration, $a = 5\,m/{s^2}$.
(b) Its speed when it was at the first point, ${u_{{P_1}}} = 15\,m/s$.
(c) The distance from the first point when it was at rest, $x = 22.5\,m$.

Note: From the diagram which is drawn as per the given instructions in the problem we can say that the journey of the car is divided into two parts. Here we take the velocity at the $1st$ point as the final velocity of the $1st$ part of the motion and, the velocity at the second point as the final velocity of the second part. Also, the final velocity of the $1st$ part is taken as the initial velocity of the $2nd$ part. Since the whole journey is with a constant acceleration, we take the same value of the acceleration for both of the two parts.The understanding of the velocity of these points is very important to do any type of problem regarding the motions.