Question

A car starting from rest accelerates at the rate of $f$ through a distance $s$ , then continues at a constant speed for time $t$ and then decelerates at the rate of $\dfrac{f}{2}$ to come to rest. If the total distance travelled is ${\text{15s}}$, then
A) $s = ft$
B) $s = \dfrac{1}{6}f{t^2}$
C) $s = \dfrac{1}{2}f{t^2}$
D) $s = \dfrac{1}{{72}}f{t^2}$

Answer 1

Here the total journey of the car can be considered in parts to obtain a better understanding. In the first part, the car starts from rest and accelerates, in the second part the car moves with constant speed and in the last part the car decelerates and comes to rest. Then Newton’s third equation of motion can be used to find the distance covered in the second and third parts.

Formulas used:
Newton’s third equation of motion is given by, ${v^2} = {u^2} + 2as$ where $v$ is the final velocity of the body, $u$ is its initial velocity, $a$ is its acceleration and $s$ is the distance covered.
The distance covered by a body is given by, $s = vt$ where $v$ is the velocity of the body and $t$ is the time taken to cover the distance.

Complete step by step answer:
Step 1: Split the total path covered by the car into three parts.
In the first part, the distance travelled by the car is given to be $s$ and the acceleration is $f$. Also as the car starts from rest, its initial velocity will be $u = 0$ . Let ${v_1}$ be the final velocity of the car as it covers the distance $s$.
In the second part, the car travels with a constant velocity which will be the final velocity of the first part i.e., ${v_1}$ for time $t$.
In the third part, the car decelerates and comes to stop. So the initial velocity of the third part will be ${v_1}$ and the final velocity of the car will be ${v_f} = 0$ .
This is sketched in the figure below.

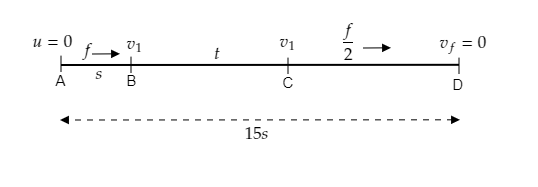
AB corresponds to the distance covered in the first part, BC corresponds to the distance covered in the second part and CD corresponds to the distance covered in the third part.
Step 2: Using Newton’s third equation of motion, obtain the final velocity ${v_1}$ of the first part.
For the first part, Newton’s equation of motion gives the final velocity as ${v_1}^2 = {u^2} + 2fs$ but as $u = 0$ we have ${v_1}^2 = 2fs$.
$\Rightarrow {v_1} = \sqrt {2fs}$
Thus the velocity at B and at C will be ${v_1} = \sqrt {2fs}$ as for the distance BC the velocity remains constant.
Step 3: Express the distance covered by the car in the second part.
The distance covered by the car in the second part will be $BC = {v_1}t$ ------- (1)
Substituting for ${v_1} = \sqrt {2fs}$ in equation (1) we get, $BC = \sqrt {2fs} t$
So the distance covered in the second part is $BC = \sqrt {2fs} t$.
Step 4: Using Newton’s third equation of motion, obtain the distance covered in the third part.
Newton’s equation of motion for the third part is given by, ${v_f}^2 = {v_1}^2 - 2\left( {\dfrac{f}{2}} \right)CD$
$\Rightarrow {v_f}^2 = {v_1}^2 - f\left( {CD} \right)$ ---------- (2)
Substituting for ${v_f} = 0$ and ${v_1} = \sqrt {2fs}$ in equation (2) we get,
$\Rightarrow 0 = 2fs - f\left( {CD} \right)$
$\Rightarrow CD = \dfrac{{2fs}}{f} = 2s$
Thus the distance covered in the third part is $CD = 2s$ .
Now the total distance covered by the car can be expressed as $AB + BC + CD = 15s$ -------- (3)
Substituting for $AB = s$ , $BC = \sqrt {2fs} t$ and $CD = 2s$ in equation (3) we get,
$\Rightarrow s + \sqrt {2fs} t + 2s = 15s$
$\Rightarrow \sqrt {2fs} t = 12s$
Squaring the above equation we get, $2fs{t^2} = 144{s^2}$
$\Rightarrow s = \dfrac{2}{{144}}f{t^2} = \dfrac{1}{{72}}f{t^2}$
Thus we obtain the relation for $s$ as $s = \dfrac{1}{{72}}f{t^2}$ .

Therefore, the correct option is D.

Note:
In the third part, the car is mentioned to be decelerating i.e., it slows down. So while writing Newton’s equation of motion for the third part we have the acceleration $\dfrac{f}{2}$ as negative and we get, ${v_f}^2 = {v_1}^2 - 2\left( {\dfrac{f}{2}} \right)CD$ . In the second part, the acceleration will be zero as the car travels at a constant speed in that part.