Question

A car, starting from rest, accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate $\frac{f}{2}$ to come to rest. If the total distance traversed is 15 S, then

• A. $S = \frac{1}{2}ft^{2}$
• B. $S = \frac{1}{4}ft^{2}$
• C. $S = \frac{1}{72}ft^{2}$
• D. $S = \frac{1}{6}ft^{2}$

Answer 1

Answer: (C)

$S = \frac{1}{72}ft^{2}$

Answer 2

Let car starts from point A from rest and moves up to point B with acceleration

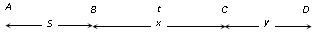
Velocity of car at point B, $v = \sqrt{2fS}$ $\lbrack As\ v^{2} = u^{2} + 2as\rbrack$

Car moves distance BC with this constant velocity in time t

$x = \sqrt{2fS}.t$ ......(i) [As $s = ut$]

So the velocity of car at point C also will be $\sqrt{2fs}$ and finally car stops after covering distance y.

Distance CD ⇒ $y = \frac{(\sqrt{2fS})^{2}}{2(f/2)} = \frac{2fS}{f} = 2S$ ....(ii)

So, the total distance AD = $AB + BC + CD$ =15S (given)

⇒ $S + x + 2S = 15S$ ⇒ $x = 12S$

Substituting the value of x in equation (i) we get

$x = \sqrt{2fS}.t$ ⇒ $12S = \sqrt{2fS}.t$ ⇒ $144S^{2} = 2fS.t^{2}$

⇒ $S = \frac{1}{72}ft^{2}$.