Question

A car P moves due to east with a speed $10\,{ms^{-1}}$ and another car Q moves due west with a speed $15\,{ms^{-1}}$. The velocity of
car P as observed by car Q is
A. $25\,{ms^{-1}}$ due east
B. $25\,{ms^{-1}}$ due west
C. $5\,{ms^{-1}}$ due east
D. $5\,{ms^{-1}}$ due west

Answer 1

The speed of both the cars is given, using those values and plotting in an x-y plane we get a clear understanding of the given situation. As both the car moves in opposite directions, therefore, one car will be in positive x-direction while the other will be in negative x-direction and then we have to find the velocity of the first car observed by the second car.

Complete step by step answer:
We will first draw a rough diagram of both cars moving in opposite directions.

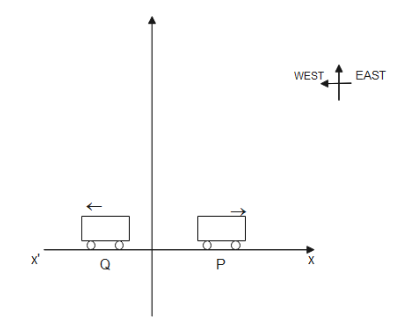
Now as we can see that car P is in positive x-direction and car Q is moving in the negative x-direction. To find the velocity of car P as observed by car Q we will add the velocities of the cars. The velocity of P with respect to Q is given by $V_{PQ}$.
$V_P=10i$ , $V_Q=-15i$
$\Rightarrow {{V}_{PQ}}={{V}_{p}}-{{V}_{Q}}$
Substituting the values we get,
$\Rightarrow {{V}_{PQ}}=10i-\left( -15i \right)$
$\therefore {{V}_{PQ}}=25i$

Therefore the speed of car P will be $25\,{ms^{-1}}$ due east.

Note: Speed is a scalar quantity. It is the distance travelled per unit time. It is not involved with any specified direction. Speed refers to how briskly an object is moving, or the rate at which the distance is covered. Velocity is a vector quantity. It has a magnitude and a specified direction. It is the rate of change within the position of the body with relevance to time. Relative velocity is the velocity of one object with respect to another object. It is the velocity between two objects calculated in a single coordinate system.