Question

A car of weight W is on an inclined road that rises by 100 m over a distance of 1 km and applies a constant frictional force $\dfrac{W}{20}$ on the car. While moving uphill on the road at a speed of 10 m/s, the car needs power P. If it needs power $\dfrac{P}{2}$ while moving downhill at speed v then value of v is:
A. 15 m/s
B. 5 m/s
C. 10 m/s
D. 20 m/s

Answer 1

It is said that a car is traveling on an inclined road and we are given the weight of the car and the friction between the car and the surface of the road. We can draw the free body diagrams when the car moves uphill and downhill. Thus we can find the force and using the equation to find power and equating the two cases in an appropriate way we will get the value of velocity when the car moves downhill.
Formula used:
$P=Fv$

Complete answer:
In the question we are given a car of weight W and it is said that the car is traveling on an inclined road that rises by 100 m over a distance of 1 km.
The figure below shows us the inclined road.

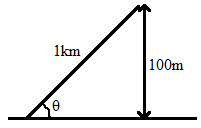
It is said that the inclination is up to a distance 1km = 1000 m.
From the figure we can see that,
$\sin \theta =\dfrac{100}{1000}$
$\Rightarrow \sin \theta =\dfrac{1}{10}$
$\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{1}{10} \right)$
That is, the angle of inclination of the road is ${{\sin }^{-1}}\left( \dfrac{1}{10} \right)$
It is said that the car is moving uphill on the road with a velocity 10m/s and the frictional force between the car and road is given as $\dfrac{W}{20}$.
The figure below shows the free body diagram when the car moves uphill.

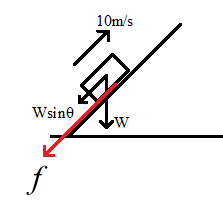
The forces acting on the car are the sine component of the weight of the car and frictional force, i.e.
$F=W\sin \theta$
$F=f=\dfrac{W}{20}$
It is said that the car requires a power P when it moves uphill.
We know that the equation for power is given as,
$P=Fv$
We have the net force her as,
$F=W\sin \theta +\dfrac{W}{20}$
And the velocity is given as 10m/s
Therefore here the power will be
$\Rightarrow P=\left( W\sin \theta +\dfrac{W}{20} \right)10$
From previous calculation we know that,
$\sin \theta =\dfrac{1}{10}$
Therefore we can write the power as,
$\Rightarrow P=\left( \dfrac{W}{10}+\dfrac{W}{20} \right)10$
Now let us consider the figure given below which shows the free body diagram when the car is moving downwards.

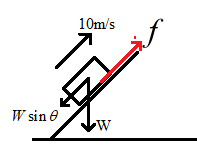
Here the frictional force is acting in the opposite direction.
Therefore the net force in this case is,
$F=W\sin \theta -\dfrac{W}{20}$
We know that power, $P=Fv$. But in the question it is said that for the car to move downhill, it requires a power $\dfrac{P}{2}$. Therefore we can write,
$\Rightarrow \dfrac{P}{2}=Fv$
By substituting for force, we will get,
$\Rightarrow \dfrac{P}{2}=\left( W\sin \theta -\dfrac{W}{20} \right)v$
Since $\sin \theta =\dfrac{1}{10}$, we can write
$\Rightarrow \dfrac{P}{2}=\left( \dfrac{W}{10}-\dfrac{W}{20} \right)v$
By substituting for P in the above equation from the first case, we will get
$\Rightarrow \left( \dfrac{\left( \left( \dfrac{W}{10}+\dfrac{W}{20} \right)10 \right)}{2} \right)=\left( \dfrac{W}{10}-\dfrac{W}{20} \right)v$
By solving this we will get the value of v as,
$\Rightarrow \dfrac{1}{2}=\dfrac{\left( \dfrac{W}{10}-\dfrac{W}{20} \right)v}{\left( \dfrac{W}{10}+\dfrac{W}{20} \right)10}$
$\Rightarrow \dfrac{1}{2}=\dfrac{\left( \dfrac{20W-10W}{10\times 20} \right)v}{\left( \dfrac{20W+10W}{10\times 20} \right)10}$
$\Rightarrow \dfrac{1}{2}=\dfrac{10W\times v}{30W\times 10}$
$\Rightarrow \dfrac{1}{2}=\dfrac{10\times v}{30\times 10}$
$\Rightarrow v=\dfrac{10\times 30}{2\times 10}$
$\Rightarrow v=\dfrac{30}{2}$
$\Rightarrow v=15m/s$
Therefore the speed of the car while moving downhill is 15m/s.

So, the correct answer is “Option A”.

Note:
In this question it is important to draw the free body diagram of the two cases. A free body diagram of a system is a diagram which shows us both the magnitude and direction of all the forces acting on that system. Thus by drawing the free body diagram it will be much easier to calculate the net force. Hence for similar questions you should construct the free body diagram.