Question

A car of mass $m$ moving over a concave bridge of radius $r$. Find the normal reaction acting on the car when it is at the lowest point of the bridge.

Answer 1

Use the expression for Newton’s second law of motion. Also use the formula for centripetal force acting on an object inn circular motion. Draw the free body diagram of the car at the lowest point on the bridge and apply Newton’s second law of motion to the car in the vertical direction. This gives the required expression for the normal reaction on the car.

Formula used:
The expression for Newton’s second law of motion is given by
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.
The centripetal force ${F_C}$ acting on an object is given by
${F_C} = \dfrac{{m{v^2}}}{R}$ …… (2)
Here, $m$ is the mass of the object, $v$ is the velocity of the object and $R$ is the radius of the circular path.

Complete step by step answer:
We have given that the car of mass $m$ is moving on a concave bridge whose radius is $r$.We have asked to determine the normal reaction or normal force acting on the car when it is at the lowest point of the bridge.Let us first draw the free body diagram of the car when it is at the lowest point of the concave bridge.

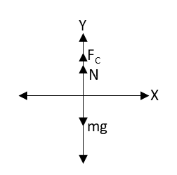
In the above free body diagram, $mg$ is weight of the car, $N$ is the normal force exerted by the bridge on the car and ${F_C}$ is the centripetal force acting on the car.The centripetal force provides the force necessary for the motion of the car on the bridge.Let us apply Newton’s second law of motion to the car on the bridge in the vertical direction.
$N - mg = {F_C}$
Substitute $\dfrac{{m{v^2}}}{r}$ for ${F_C}$ in the above equation.
$N - mg = \dfrac{{m{v^2}}}{r}$
$\therefore N = mg + \dfrac{{m{v^2}}}{r}$
This is the expression for the normal reaction of the bridge on the car moving on it at the lowest point of bridge.

Note: The students should keep in mind that the centripetal force acting on the car provides the necessary force for the motion of the car on the bridge as the acceleration of the car on the bridge is equal to centripetal acceleration of the car. It should be taken on the right hand side of the expression for Newton’s second law of motion and not on the left hand side.