Question

A car of mass ‘m’ is driven with acceleration ‘a’ along a straight level road with a constant external resistive force ‘R’, when the velocity of car is ‘V’, the rate at which the engine is doing work will be-
$\text{A}\text{. RV}$
$\text{B}\text{. maV}$
$\text{C}\text{. (R+ma)V}$
$\text{D}\text{. (ma-R)V}$

Answer 1

Hint: The force required for the car to keep it in motion with acceleration ‘a’ must oppose the resistive force ‘R’ and ‘V’ is the instantaneous velocity of the car. Resistive force ‘R’ is externally acting that means this force is only due air resistance against the motion of the car.

Complete step-by-step answer:

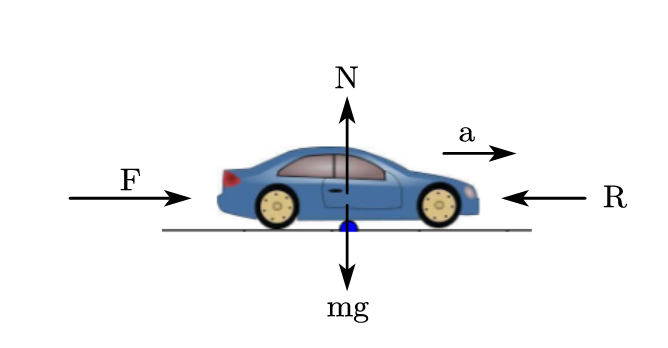
The force required for car to be in motion will be
$F=R+ma$
We know that the rate of doing work per unit time is known as power. So ultimately, we have to calculate power which is delivered by the engine of the car.
$P=F\times V$
Here, P is power which is delivered
F is the driving force
V is the velocity of car
Therefore, power that must be delivered by car engine will be
$P=(R+ma)V$

Additional Information:
In real situations, the power that is delivered by the engine of a car is not fully transferred to the motion of the car. There are many losses and irreversibility such as frictional losses between wheels and tires, heat generation among moving components, air resistance and gradient of road.
But such losses are not to be neglected in practical situations which makes them complicated to solve.

Note: The acceleration ‘a’ of a car is actually the resultant of applied force ‘F’ and resistive force ‘R’ with neglecting all the resistances. We can also verify the answer by equating dimensions of L.H.S to dimensions of R.H.S.