Question

A car moving towards the south with a speed of $20\dfrac{m}{s}$. A motorcyclist is moving towards the east with a speed of $15\dfrac{m}{s}$. At a certain instant (t=0) the motorcyclist is due south of the car and is at a distance of $50{\text{m}}$ from the car. The shortest distance between the motorcyclist and the car is and which they are nearest to each other after t=0.
A) $10{\text{m}}$, $1 \cdot 6s$.
B) $20{\text{m}}$, $1s$.
C) $30{\text{m}}$, $1 \cdot 6s$.
D) $40{\text{m}}$, $1s$.

Answer 1

The vector resultant can be used here to solve this problem. As the resultant can be moved from one place to another without changing its orientation. Also, the negative of the vector is the vector having the same magnitude and the direction is just opposite to the original vector.

Complete step by step answer:
As it is given that the car is moving south with a speed of $20\dfrac{m}{s}$ and the motorcyclist is moving towards the east with a speed of $15\dfrac{m}{s}$.

Let us change the direction of the velocity vector of the car and then calculate the resultant of the velocities of the car and motorist.

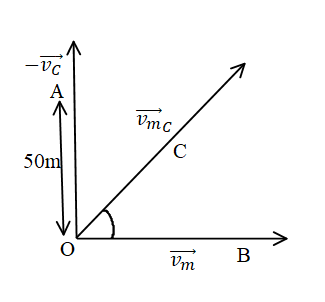
As it is also given that the distance between the car and motorist initially was 50m.
Now the resultant of the velocity vector of car velocity and motorist velocity is given by,
$\Rightarrow {\overrightarrow v _{mc}} = \sqrt {{{15}^2} + {{20}^2}}$
$\Rightarrow {\overrightarrow v _{mc}} = \sqrt {625}$
$\Rightarrow {\overrightarrow v _{mc}} = 25\dfrac{m}{s}$
Now calculate the angle,
$\Rightarrow \tan \theta = \left( {\dfrac{{{v_c}}}{{{v_m}}}} \right)$
$\Rightarrow \tan \theta = \left( {\dfrac{{20}}{{15}}} \right)$
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{{20}}{{15}}} \right)$
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {1 \cdot 33} \right)$
$\Rightarrow \theta = 53^\circ$
The shortest distance will be perpendicular from the point A to the resultant of the velocity vector of car and motorist.

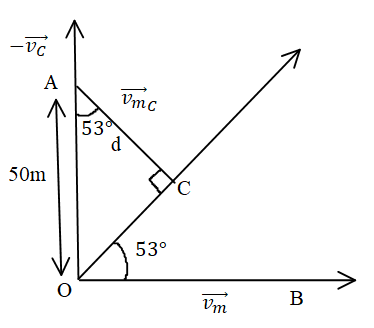
The shortest distance is $d$ to the resultant of the velocity vector of car and motorist.
Here the shortest distance is given by,
In the above triangle formed.
$\Rightarrow 50\cos 53^\circ = d$
$\Rightarrow d = 30m$.
So the shortest distance is given by $d = 30m$.
Now let us calculate the time taken by the motorist to reach point C is given by,
As ${\text{OM}} = 50\sin 53^\circ$and${\overrightarrow v _{mc}} = 25\dfrac{m}{s}$.
The time taken is given by ${\text{time}} = \dfrac{{{\text{distance}}}}{{{\text{speed}}}}$
So the time is given by,
$\Rightarrow t = \dfrac{{{\text{OC}}}}{{\left| {{{\vec v}_{mc}}} \right|}}$
$\Rightarrow t = \dfrac{{50\sin 53^\circ }}{{25}}$
$\Rightarrow t = 1.6s$

$\therefore$ The shortest distance is given by $d = 30m$ and the time taken by the motorist is equal to $t = 1.6s$. So the correct option for this problem is option (C).

Note:
The initial distance between the motorist and the car was 50m also when we change the direction of any vector completely opposite to its initial direction then a negative sign comes while representing the new vector.