Question

A car moving on a straight path covers a distance of 1 km due east in 100 s. Find the velocity of the car.
A) $10{\text{m}}{{\text{s}}^{ - 1}}$ due west.
B) $10{\text{m}}{{\text{s}}^{ - 1}}$ due east.
C) $10{\text{m}}{{\text{s}}^{ - 1}}$ due south.
D) $10{\text{m}}{{\text{s}}^{ - 1}}$ due north.

Answer 1

Velocity is a vector quantity and thus will have both magnitude and direction. The magnitude part of the velocity refers to how fast the car is moving while the direction part refers to the direction in which the car is headed. It is the displacement of the car over time.

Formula used:
The velocity of an object in motion is given by, $v = \dfrac{d}{t}$ where $d$ is the displacement of the object and $t$ is the time taken to cover that displacement.

Complete step by step answer:
Sketch a graph depicting the motion of the car and list the parameters mentioned in the question.

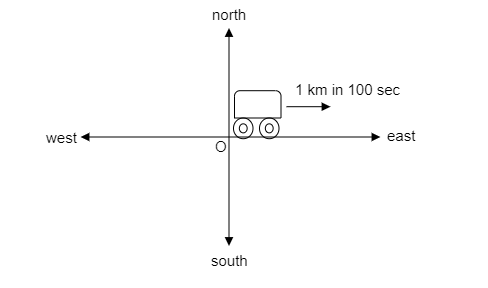
In the above figure, north is taken to be along the positive y-direction, south is along the negative y-direction, east is along the positive x-direction and west is along the negative x-direction.
The distance travelled by the cover is given to be $s = 1{\text{km}}$ and the time taken to cover that distance is $t = 100{\text{s}}$ .
The displacement of the car will be equal to the distance covered by the car.
Thus if $d$ is the displacement of the car, then it will be $d = s = 1{\text{km}}$ and directed due east.
Let $v$ be the velocity with which the car travels.
Express the relation for the velocity of the car.
The velocity of the car in motion is given by, $v = \dfrac{d}{t}$ ------- (1)
where $d$ is the displacement of the object and $t$ is the time taken to cover that displacement.
Substituting the values for $d = 1000{\text{m}}$ and $t = 100{\text{s}}$ in equation (1) we get, $v = \dfrac{{1000}}{{100}} = 10{\text{m}}{{\text{s}}^{ - 1}}$
Thus the magnitude of the velocity of the car is $v = 10{\text{m}}{{\text{s}}^{ - 1}}$ .
Since it is mentioned that the car moves in a straight path it is headed due east.

$\therefore$ The correct option is B.

Note:
Displacement of the car refers to the difference between the final position and the initial position of the car. Here, as the car never changed its direction of motion, the displacement is the same as that of the distance covered. While substituting the values for different physical quantities in any equation make sure that all the quantities are expressed in their respective S.I. units. If not, then the necessary conversion must be done. Here the displacement $d$ is given in kilometres, so it is converted to meters as $d = 1000{\text{m}}$ before substituting in equation (1).