Question

A car moving at $160km/h$ when passes the mark. A driver applies the brake and reduces its speed uniformly to $40km/h$ at the mark $C$. The marks are spaced at equal distances along the road as shown below.
At which part of the track the car has instantaneous speed of $100km/h$? Neglect the size of the car.

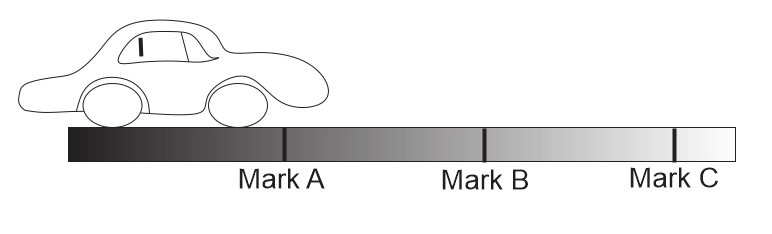
A. At mark B
B. Between mark A and mark B
C. Between mark B and mark C
D. Insufficient information to decide.

Answer 1

Use laws of motion and concept of inequality to solve this question. Assume some point $D$ at which speed is $100km/hr$ and then compare it with point $B$ and $C$.

Formula used: ${v^2} = {u^2} = 2as$

Complete step by step answer:
In the question, it is given that the initial velocity of the car is
$u = 160km/hr$
Final velocity of the car at point$C$is
$v = 40km/hr$
$AB = AC$
Let the retardation after applying brakes be a consider a motion of car from point $A$ to point $C$ we know that
${v^2} - {u^2} = 2as$ . . . (1)
Where, $v$ is final velocity
$u$ is initial velocity
$a$ is acceleration
$s$ is displacement
By substituting the given values in above equation we get,
${40^2} - {160^2} = 2( - a)s$ {$\therefore$retardations negative acceleration}
By rearranging it, we get
$- zaAC = (40 - 160)(40 + 160)$
Since, $s = AC$and${a^2} - {b^2} = (a + b)(a - b)$
$\Rightarrow - 2aAC = - 120 \times 200$
$\Rightarrow aAC = 60 \times 200$ . . . (2)
Now, let us say that the instantaneous speed of the car ${v_i} = 100km/hr$is at some point $D$.
Then, again using equation (1), we can write
${100^2} - {160^2} = 2( - a)AD$
Since, $s = AD,$
Retardation is uniform and initial velocity will be the same
$u = 160km/hr$
On simplifying the above equation, we get
$- 2aAD = (100 - 160)(100 + 160)$
$(\because {a^2} - {b^2} = (a - b)(a + b)$
$\Rightarrow - 2aAD = - 60 \times 260$
$\Rightarrow aAD = 30 \times 260$ . . . (3)
By dividing equation (2) by equation (3), we get
${{aAC}}{{aAD}} = \dfrac{{60 \times 200}}{{30 \times 260}}$
On simplifying it, we get
$\dfrac{{AC}}{{AD}} = \dfrac{{400}}{{260}}$
$= \dfrac{{40}}{{26}}$
$\dfrac{{AC}}{{AD}} = \dfrac{{20}}{{13}} > 1$ . . . (4)
Since, numerator$B$greater than denominator
$\Rightarrow AC > AD$
Therefore, we can conclude that$D$must be between$A$and$C.$
Now, $AC = AB + BC$
$\Rightarrow AC = 2AB(\because Ab = BC)$
Equation (4) becomes
$\dfrac{{2AB}}{{AD}} = \dfrac{{20}}{{13}}$
$\Rightarrow \dfrac{{AB}}{{AD}} = \dfrac{{10}}{{13}} < 1$ (since, denominator is greater than numerator)
$\Rightarrow AB < AD.$
Therefore, we can conclude that the point must be after $B.$
i.e. $D$ lies between $B$ and $C.$

So, the correct answer is “Option C”.

Note:
we only need to compare point $D$ with point $B$ and $C$. It is not asked to find the exact distance of point $D$ so, do not waste time in calculating the exact value of $\dfrac{{20}}{{13}}$. Know that compassion can be done using inequalities. Calculating ${40^2}$ and $160^\circ$, and then subtracting them could be lengthy and you can make mistakes. Use formulas to simplify such calculations.