Question

A car moves with speed $60km/h$ for $1$ hour in east direction and with same speed for $30\min$in south direction. The displacement of car from initial position is:
A. $60km$
B. $303km$
C. $30\sqrt 5 km$
D. $60\sqrt 2 km$

Answer 1

Calculate the displacement in the both the directions using the formula of displacement. Then use Pythagoras theorem to find the required solution.

Formula used:
$s = vt$ . . . (1)
Where,
$s$ is the displacement
$v$ is velocity
$t$ is time

Complete step by step answer: Observe the diagram

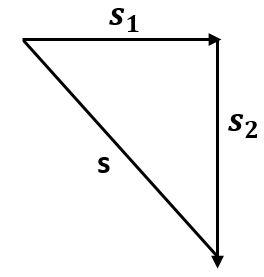
Let ${s_1}$ be the displacement in the east direction with velocity ${v_1}$ and time ${t_1}$
It is given in the question that
${v_1} = 60km/h$ and
${t_1} = 1h$
Therefore, from equation (1), we get
${s_1} = {v_1}{t_1}$
$= 60 \times 1$
$\Rightarrow {s_1} = 60km$
Now, let ${s_2}$ be the displacement in the east direction with velocity ${v_2}$ and time ${t_2}$
It is given in the question that that the car maintained the same speed while travelling the distance ${s_2}$
And the time taken is ${t_2} = 30\min = \dfrac{1}{2}h$
${s_2} = {v_2}{t_2}$
$= 60 \times \dfrac{1}{2}$
${s_2} = 30km$
Now, by observing the diagram and using Pythagoras theorem, we can say that the total displacement by the car is
$s = \sqrt {s_1^2 + s_2^2}$
$= \sqrt {{{60}^2} + {{30}^2}}$
$= \sqrt {3600 + 900}$
$= \sqrt {4500}$
$\Rightarrow s = 30\sqrt 5 km$
Therefore, the total displacement done by the car is $30\sqrt 5 km$
Therefore, from the above explanation, the correct answer is, option (C) $30\sqrt 5 km$

Note: The formula used in this question is very easy. The question does not depend on the formula. It depends on the concept that the displacement is the shortest distance between two points. So to solve this question, you should know that the angle between the two given displacements would be ${90^0}$ and hence, we can use Pythagoras theorem to solve this question.