Question
Question: A car moves in a single track of radius \[4\,{\text{m}}\] at a constant speed of \[2\,{\text{m}}{{\t...
A car moves in a single track of radius 4m at a constant speed of 2ms−1 from A and B as shown in figure. The acceleration of car at the position halfway between A and B is:
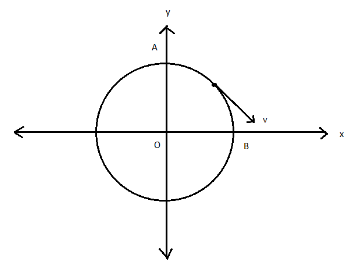
(A) −21(i^+j^)
(B) 21(i^+j^)
(C) −(i^+j^)
(D) Zero
Solution
First of all, we will draw the diagram which relates the question, then we will calculate the acceleration by the formula. After that we will write the acceleration in vector form by taking one component along the vertical axis and the other along the horizontal axis.
Complete step by step answer:
In the given problem, we are supplied with the following data:
The radius of the track in which the car is moving is 4m .
The speed of the car is 2ms−1 .
We are asked to find the acceleration of the car at the position which is halfway between A and B.
To solve this problem, we will draw a diagram for better understanding.
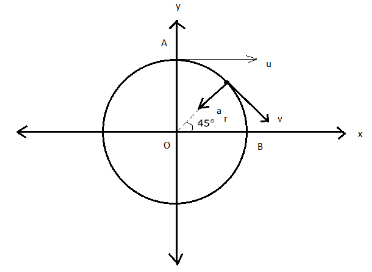
In the question we are asked to find out the acceleration at halfway, so the angle subtended by the car at the centre of the circular track will definitely be 45∘ . We have added initial velocity to be u . The acceleration that we require is directed inside symbolised as ar .
Now, we find the magnitude of the acceleration, which is given by the formula:
ar=Rv2 …… (1)
Where,
ar indicates the acceleration at the halfway point.
v indicates the velocity at which the car is moving.
R indicates the radius of the circular track.
Substituting the required values in the equation (1), we get:
We add up another diagram which consists only the required acceleration and its components, as given below:
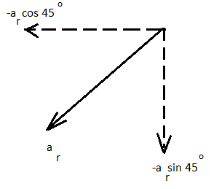
Now, we write the acceleration in the vector form.
As we can see in the diagram that if the direction of acceleration is counted then both its horizontal component and vertical component will be along the negative axes.
Hence, the vector form of the acceleration is found to be −21(i^+j^) .
The correct option is A.
Note: While solving this problem, you should have a good knowledge of vectors and its respective components. The acceleration is directed inside and for this reason the components will be along the negative axes. Writing the vector form with positive components will definitely affect the result obtained.
