Question

A car moves $40m$ east then, turns towards north and moves $30m$, turns ${45^ \circ }$ east of north moves $20\sqrt 2 m$. Given that, east is the positive $x - axis$ and north is positive $y - axis$. Find the net displacement of the car.
(A) $50\hat i + 60\hat j$
(B) $60\hat i + 50\hat j$
(C) $30\hat i + 40\hat j$
(D) $40\hat i + 30\hat j$

Answer 1

Hint Find all the required distances travelled by the car for calculating the et displacement by using the Pythagoras theorem. Some of them can also be founded by using the –
$\Rightarrow$

$$\sin \theta = \dfrac{{Perpendicular}}{{Hypoteneuse}} \\\ \cos \theta = \dfrac{{Base}}{{Hypoteneuse}} \\\$$

Step by Step Solution
The map of travelling of the car can be shown in the figure –

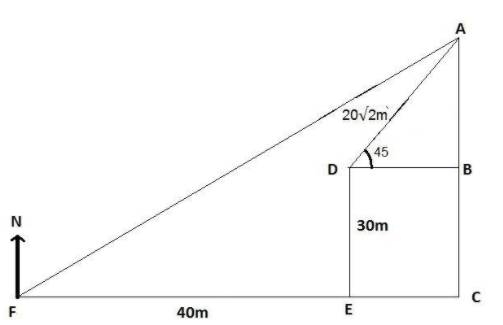
From the figure,
We can conclude that $F$ is the starting position of the car and $A$ is the finishing position of the car. So, the net displacement of the car is $FA$.
Distance of $CE$ is equal to the distance of $BD$.
Therefore, in triangle $ABD$-
$\Rightarrow$ $\cos \theta = \dfrac{{Base}}{{Hypotenuse}} \\\ \cos \theta = \dfrac{{BD}}{{AD}} \\\$
Now, putting the values of base and hypotenuse from the triangle $ABD$-
$\Rightarrow$ $\cos {45^ \circ } = \dfrac{{BD}}{{AD}} \\\ \Rightarrow BD = AD\cos {45^ \circ } \\\ BD = 20\sqrt 2 \times \dfrac{1}{{\sqrt 2 }} \\\$
Cancelling $\sqrt 2$ on numerator and denominator, we get –
$\Rightarrow$ $BD = 20m$
Now, the distance $FC$ can be calculated by –
$\Rightarrow$ $FC = FE + EC \\\ FC = 40m + BD \\\ \therefore FC = 40 + 20 = 60m \\\$
In the figure, we can see that –
$\Rightarrow$ $DE = BC \\\ \because DE = 30m \\\ \therefore BC = 30m \\\$
Again, in triangle $ABD$-
$\Rightarrow$ $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}} \\\ \sin \theta = \dfrac{{AB}}{{AD}} \\\ \Rightarrow AB = AD\sin \theta \\\$
Putting the values from the question –
$\Rightarrow$ $AB = 20\sqrt 2 \sin {45^ \circ } \\\ AB = 20\sqrt 2 \times \dfrac{1}{{\sqrt 2 }} \\\ AB = 20m \\\$
So, $AC$ can be calculated as –
$\Rightarrow$ $AC = AB + BC \\\ AC = 20 + 30 = 50m \\\$
We know that, Pythagoras theorem is –
$\Rightarrow$ $Hypotenuse = \sqrt {{{\left( {Perpendicular} \right)}^2} + {{\left( {Base} \right)}^2}}$
Now, in triangle $AFC$ -
Using the Pythagoras theorem, we get –
$\Rightarrow$ $AF = \sqrt {{{\left( {FC} \right)}^2} + {{\left( {AC} \right)}^2}} \cdots \left( 1 \right)$
We already got the values for $FC$ and $AC$
Therefore, putting the values of $FC$ and $AC$ in equation $\left( 1 \right)$, we get –
$\Rightarrow$ $AF = \sqrt {{{\left( {60} \right)}^2} + {{\left( {50} \right)}^2}} \\\ AF = \sqrt {3600 + 2500} \\\ AF = \sqrt {6100} \\\ AF = 78.10m \\\$
Hence, we got the net displacement travelled by the car. Now, to find the angle –
$\Rightarrow$ $\tan AFC = \dfrac{{AC}}{{FC}} \\\ \tan AFC = \dfrac{{50}}{{60}} = \dfrac{5}{6} \\\$
To calculate angle $AFC$, we have to find the inverse of $\tan$-
$\Rightarrow$ $angle\left( {AFC} \right) = {\tan ^{ - 1}}\left( {\dfrac{5}{6}} \right) \\\ angle\left( {AFC} \right) = {40^ \circ } \\\$
$\Rightarrow {90^ \circ } - {40^ \circ } = {50^ \circ }$
Hence, the net displacement travelled by the car is $78.1m$ and is ${50^ \circ }$ east.
As given in question, $x - axis$ is the east. So, it is denoted by $\hat i$
Hence, the net displacement will be $50\hat i + 60\hat j$.

Therefore, the correct option is (A).

Note Pythagoras theorem states that, “in a triangle the square of hypotenuse is equal to the addition of square of perpendicular and square of base”. This method is used when the triangle is right – an angled triangle. It is useful when we know the two sides of the triangle, then, we can easily know the third side of the triangle.