Question

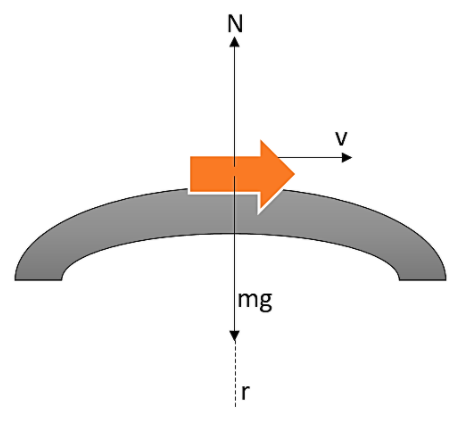
A car is travelling over a flyover bridge which is a part of a vertical circle of radius $10m$. At the highest point of it, when the normal reaction on the car is half of its weight, then the speed of the car will be:
$\begin{aligned} & A.7m{{s}^{-1}} \\\ & B.10m{{s}^{-1}} \\\ & C.14m{{s}^{-1}} \\\ & D.20m{{s}^{-1}} \\\ \end{aligned}$

Answer 1

Here it is told that the normal reaction is half of its weight. Compare both these conditions. Then find out the net force provided by the centripetal force. Substitute the value of normal reaction with the compared value. And then find out the speed of the car after necessary rearrangements.

Complete answer:
First of all let us talk about the values mentioned in the question.
The radius of the vertical circle travelled by the car is given as,
$R=10m$
Here it is mentioned already that the normal reaction of the car is equivalent to the half of the weight of the car. This can be written in mathematical form as,
$N=\dfrac{mg}{2}$
Where $m$ be the mass of the car and $g$ be the acceleration due to gravity.
Therefore the net force provided by the car will be given as,
$mg-N=\dfrac{m{{v}^{2}}}{R}$
The net force acting on the body will be equivalent to the centripetal force in order to traverse the vertical circle.
Here we can substitute the value of normal reaction in this,
$mg-\dfrac{mg}{2}=\dfrac{m{{v}^{2}}}{R}$
Let us rearrange the obtained equation in terms of $v$,
$\dfrac{mg}{2}=\dfrac{m{{v}^{2}}}{R}$
Cancelling the similar terms in the equation,
$v=\sqrt{\dfrac{Rg}{2}}$
Substituting the values in it,
$v=\sqrt{\dfrac{10\times 9.8}{2}}=7m{{s}^{-1}}$

Therefore the correct answer is option A.

Note:
As the centripetal force is experienced upon a body which is in motion along a circle at a fixed speed, the force will always be felt inwards because the velocity of the body is directed tangential to the circle. Therefore, the work performed by the centripetal force in a uniform circular motion is zero.