Question

A car is travelling on a straight road along a field. A person standing at a distance $'d'$ from the road. If the speed of the car is ‘u’ and the actual frequency of its horn is ‘$f_0$’ then the frequency heard by the observer when the car is closest to him is (the velocity of sound in air is v)
(A) ${{f}_{0}}$
(B) ${{f}_{0}}\dfrac{v}{c}$
(C) ${{f}_{0}}\left[ \dfrac{{{v}^{2}}}{{{v}^{2}}-{{u}^{2}}} \right]$
(D) ${{f}_{0}}\left[ \dfrac{{{v}^{2}}-{{u}^{2}}}{{{v}^{2}}} \right]$

Answer 1

The questions about moving sources or observers of sound with words like apparent frequency being used belong to the unit – Doppler’s effect. There is a very simple method of solving such problems using the formula${{f}_{0}}=f\left[ \dfrac{{{v}_{O}}}{{{v}_{S}}} \right]$where ${{f}_{0}}$ is the apparent frequency, $f$is the source frequency, ${{v}_{O}}$ is the velocity of sound relative to observer and ${{v}_{S}}$ is the velocity of sound relative to the source.

Complete step by step answer:
Since our observer is stationary, velocity of sound relative to the observer = velocity of sound itself = v (given)

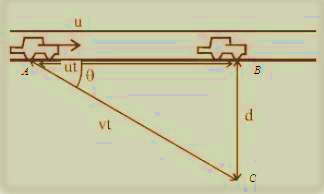
Now, velocity of sound relative to source = $=v-u\cos \theta$
Substituting the values back in our formula, $f={{f}_{0}}\dfrac{v}{v-u\cos \theta }$
From the diagram above, we can say that

& \cos \theta =\dfrac{ut}{vt}=\dfrac{u}{v} \\\ & f={{f}_{0}}\dfrac{v}{v-u\dfrac{u}{v}}={{f}_{0}}\dfrac{{{v}^{2}}}{{{v}^{2}}-{{u}^{2}}} \\\ \end{aligned}$$ **Note:** Doppler Effect was discovered by Christian Johann Doppler refers to the change in wave frequency during a relative motion between a wave source and its observer. We can get a variety of questions in Doppler effect, sometimes the source is moving away from the observer, sometimes it’s moving towards the observer and most of the time, both the source and the observer are moving relative to each other. The good news for you is, you only need one formula to solve any question of Doppler Effect, which is $${{f}_{0}}=f\left[ \dfrac{{{v}_{O}}}{{{v}_{S}}} \right]$$, and the only thing you need to be careful is finding out the relative velocity of sound with respect to the observer and the source.