Question

A car is moving with constant speed on a rough banked road.

Figure shows the free body diagram of car in three situation A, B & C

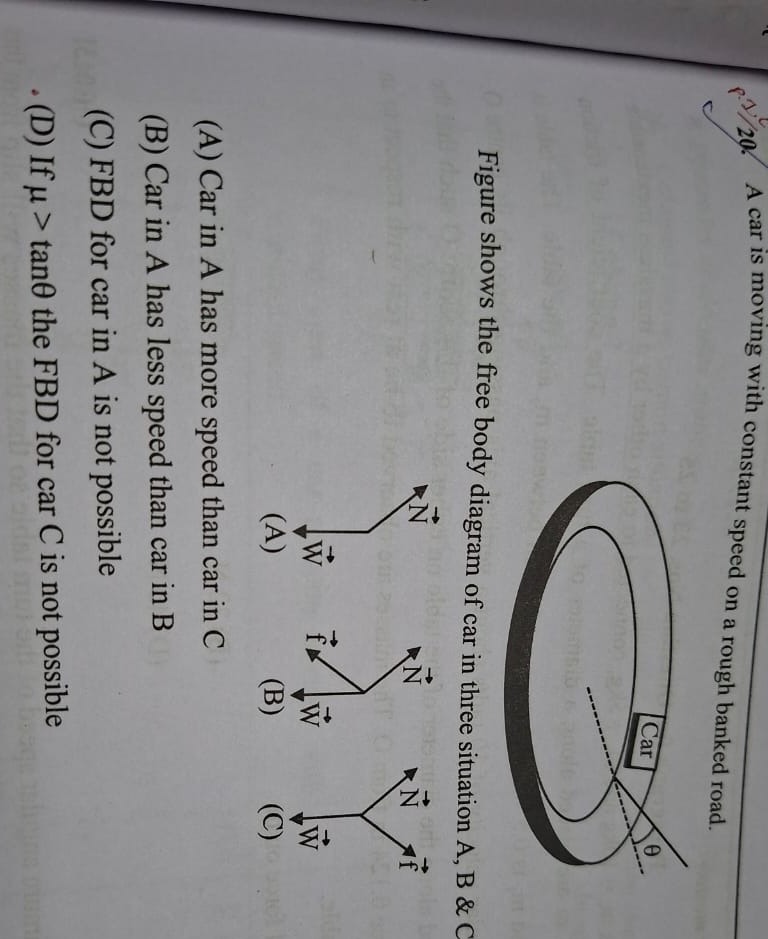
• A. Car in A has more speed than car in C
• B. Car in A has less speed than car in B
• C. FBD for car in A is not possible
• D. If $\mu$ > tan$\theta$ the FBD for car C is not possible

Answer 1

Answer: (D)

If $\mu$ > tan$\theta$ the FBD for car C is not possible

Answer 2

The problem analyzes the forces acting on a car on a rough banked road. We need to determine the correctness of the given statements based on the free-body diagrams (FBDs) and the conditions for motion on a banked road.

Let $v_0 = \sqrt{gR \tan\theta}$ be the critical speed where banking alone provides the centripetal force and friction is zero.

FBD (A): Friction is directed downwards. This occurs when the car's speed $v_A > v_0$. For downward friction, the condition for not slipping downwards (with maximum friction $f = \mu N$) is: $N \sin\theta - \mu N \cos\theta \ge \frac{mv_A^2}{R}$ The vertical equilibrium condition is: $N \cos\theta = mg + \mu N \sin\theta$ $N(\cos\theta - \mu \sin\theta) = mg$ $N = \frac{mg}{\cos\theta - \mu \sin\theta}$ For a positive normal force $N$, we need $\cos\theta - \mu \sin\theta > 0$, which means $\cot\theta > \mu$, or $\tan\theta > 1/\mu$. If $\tan\theta < \mu$, then $\cos\theta - \mu \sin\theta < 0$. In this case, even with maximum upward friction, the net horizontal force would not be enough to provide the centripetal force. However, for downward friction, the condition for not slipping upwards is: $N \sin\theta - f \cos\theta \ge \frac{mv_A^2}{R}$ The vertical equilibrium is: $N \cos\theta + f \sin\theta = mg$ With maximum downward friction $f = \mu N$: $N \cos\theta + \mu N \sin\theta = mg$ $N(\cos\theta + \mu \sin\theta) = mg$ $N = \frac{mg}{\cos\theta + \mu \sin\theta}$ The centripetal force condition becomes: $\frac{mg \sin\theta}{\cos\theta + \mu \sin\theta} - \frac{\mu mg \cos\theta}{\cos\theta + \mu \sin\theta} \ge \frac{mv_A^2}{R}$ $\frac{mg(\sin\theta - \mu \cos\theta)}{\cos\theta + \mu \sin\theta} \ge \frac{mv_A^2}{R}$ For $v_A^2$ to be positive, we need $\sin\theta - \mu \cos\theta > 0$, which means $\tan\theta > \mu$. So, FBD (A) is possible if $\tan\theta \ge \mu$. If $\tan\theta < \mu$, FBD (A) is not possible.

FBD (C): Friction is directed upwards. This occurs when the car's speed $v_C < v_0$. For upward friction, the condition for not slipping downwards (with maximum friction $f = \mu N$) is: $N \sin\theta + \mu N \cos\theta \ge \frac{mv_C^2}{R}$ The vertical equilibrium condition is: $N \cos\theta = mg + \mu N \sin\theta$ $N(\cos\theta - \mu \sin\theta) = mg$ $N = \frac{mg}{\cos\theta - \mu \sin\theta}$ For a positive normal force $N$, we need $\cos\theta - \mu \sin\theta > 0$, which means $\cot\theta > \mu$, or $\tan\theta > 1/\mu$. If $\tan\theta \le 1/\mu$ (i.e., $\mu \ge \cot\theta$ or $\mu \ge 1/\tan\theta$), then $\cos\theta - \mu \sin\theta \le 0$. This means that even with maximum upward friction, the car will slip downwards. Therefore, if $\tan\theta \le 1/\mu$, FBD (C) is not possible. This is equivalent to saying: If $\mu \ge \cot\theta$, FBD (C) is not possible. Or, if $\mu > \tan\theta$, FBD (C) is not possible.

Now let's evaluate the options:

(A) Car in A has more speed than car in C: FBD (A) implies $v_A > v_0$. FBD (C) implies $v_C < v_0$. If both FBDs are possible, then $v_A > v_0 > v_C$, so $v_A > v_C$. However, both FBDs may not be possible simultaneously depending on $\mu$ and $\theta$. For example, if $\tan\theta < \mu$, FBD (A) is not possible. Thus, this statement is not always true.

(B) Car in A has less speed than car in B: FBD (A) implies $v_A > v_0$. FBD (B) implies $v_B < v_0$. So, $v_A > v_0 > v_B$, which means $v_A > v_B$. The statement claims $v_A < v_B$, which is false.

(C) FBD for car in A is not possible: This statement is true only if $\tan\theta < \mu$. It is not universally true for all possible values of $\mu$ and $\theta$.

(D) If $\mu > \tan\theta$ the FBD for car C is not possible: As derived above, if $\mu > \tan\theta$, then $\tan\theta < 1/\mu$. This condition makes the minimum speed $v_{min}$ for upward friction not real, meaning upward friction is not possible. Therefore, FBD (C) is not possible. This statement is correct.

The question asks for the correct statement. Statement (D) is a correct conditional statement about the impossibility of FBD (C) under a specific condition.